I’m excited to be able to announce that today we’re releasing Mathematica 9—and it’s big! A whole array of new ideas and new application areas… and major advances along a great many algorithmic frontiers.
Next year Mathematica will be 25 years old (and all sorts of festivities are planned!). And in that quarter century we’ve just been building and building. The core principles that we began with have been validated over and over again. And with them we’ve created a larger and larger stack of technology, that allows us to do more and more, and reach further and further.
From the beginning, our goal has been an ambitious one: to cover and automate every area of computational and algorithmic work. Having built the foundations of the Mathematica language, we started a quarter century ago attacking core areas of mathematics. And over the years since then, we have been expanding outward at an ever-increasing pace, conquering one area after another.
As with Wolfram|Alpha, we’ll never be finished. But as the years go by, the scope of what we’ve done becomes more and more immense. And with Mathematica 9 today we are taking yet another huge step.
So what’s new in Mathematica 9? Lots and lots of important things. An amazing range—something for almost everyone. And actually just the very size of it already represents an important challenge. Because as Mathematica grows bigger and bigger, it becomes more and more difficult for one to grasp everything that’s in it.
But in Mathematica 9 there’s an important new idea. We call it the Wolfram Predictive Interface™, and what it does is to automate the process of suggesting at every step what to do next. At the most basic level, when you type, there’s a context-sensitive Input Assistant that knows about all the functions and options of Mathematica. But more important, when you get output, there’s a Suggestions Bar that’s generated, with a series of buttons for top actions you might want to take next. Sometimes these buttons apply individual Mathematica functions, and sometimes they do more complex things, bringing up interactive panels if need be.
Experienced software users may be skeptical. They may be thinking: “I’ve seen these kinds of heuristic let-me-help-you systems before; typically they just get in the way”. Well, I’m happy to say that I think with the Predictive Interface in Mathematica 9 we’ve made a breakthrough. Of course, it helps that we have all that experience—and all those query logs—from Wolfram|Alpha. But the result is that even for an experienced Mathematica user like myself, the Predictive Interface really does well, and it makes my use of Mathematica substantially better. And for people new to Mathematica, I think it’ll be a game-changer. Never again will they be left in a “so what do I do next?” state; they’ll always be given suggestions about how to move forward, as well as automatically be shown what’s possible in Mathematica.
There are all sorts of other interface enhancements in Mathematica 9 too. But what about the computational capabilities of Mathematica? What’s new there in Mathematica 9?
Here’s an immediate “crowd pleaser”: social network analysis. There’s now a function in Mathematica that lets you instantly get data from the APIs of popular social networks—that you can then immediately visualize and analyze using all the capabilities of Mathematica, including many new graph theoretical and statistical functions especially added in Mathematica 9 for social networks. A couple of months ago we introduced Wolfram|Alpha Personal Analytics for Facebook—which has become a highly popular service. Now we’re introducing general, programmable, social network analysis in Mathematica—which promises to be very valuable not only for professional data scientists, but also for math and computer science students who want to jump immediately to the frontiers of one of the hottest current areas.
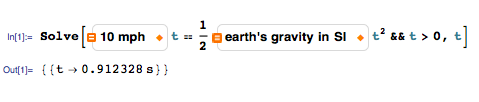
Over the last 25 years there have been a few requests for new features in Mathematica that just keep on coming in over and over again. One of those is for Mathematica to support units—like centimeters and gigabytes. Early on we created an add-on package that did just fine for simple cases, and that many people have been happily using for ages. But try as we might, we never figured out how to do a true “Mathematica-class” job of supporting units—and so we never built them into the core of the system.
Well, one feature of Wolfram|Alpha is that it includes by far the most complete handling of units ever. I used to think units were comparatively simple. But I now know they’re messy and complicated, not least because to be at all usable in practice, people have to be able to refer to them with all sorts of weird short notations. Now here’s the great thing we realized in Mathematica 9: we can just use Wolfram|Alpha-based free-form linguistics to let people enter units however they feel like. But then we can turn the units into precise symbolic expressions—that we can then support throughout Mathematica, not just in simple arithmetic, but in calculus, visualization, data analysis, and much more. And so, after all these years, in Mathematica 9 we finally have units built in—not as some kind of hack, but in a really clean, streamlined and long-term way.
Mathematica has a vast web of interconnected computational capabilities. And in each new version, we build on what is already there to reach and cover still more areas. And to me a remarkable aspect of this is just how much needs to already exist in Mathematica to be able to reach and successfully cover these new areas. Sometimes there may be some fairly easy way to implement simple examples of a new capability. But to get really good thorough coverage needs the whole stack that we’ve spent 25 years building up.
And whenever we tackle a new area in Mathematica, we try to do it to full depth and breadth. Usually this means we have to figure out all sorts of new ideas and algorithms. And often a whole new way of looking at the area. That typically dramatically clarifies the area, and both makes it accessible to a much wider class of people, and allows it to be successfully used as a long-term building block in the further development of Mathematica.
In Mathematica 9, we’ve covered quite a collection of new areas.
One example, from a “classic” Mathematica area, concerns differential equations. In Wolfram SystemModeler, we handle all sorts of systems described by differential equations. In Mathematica 9, we’ve now built in capabilities for solving differential equations with discontinuities (e.g. for a ball bouncing on a surface), hybrid discrete/continuous equations, and parametric and eigenvalue differential equations. Back in the 1970s I remember writing a Fortran program to solve an eigenvalue version of the Schrödinger equation; now finally in 2012 it’s little more than a one-liner in Mathematica 9.
There are a whole collection of new capabilities in Mathematica 9 around statistical systems and statistical modeling. We’ve been gradually building towards these for several versions. In Mathematica 7 we introduced all sorts of statistical distributions, and all sorts of methods for fitting data. Then in Mathematica 8 we introduced a very clean symbolic formalism for handling probabilities and probability distributions—as well as filling out a wide range of statistical analysis capabilities. And in Mathematica 9 we’re now extending from probability distributions to a full range of random processes.
We’re covering time series, Markov chains, queues, reliability, survival, stochastic differential equations, random graphs, and more. It’s all very clean and very unified. In each case, there’s a symbolic way to represent a model. And then it’s quite beautiful how everything fits together. Say you’ve got some data. In Mathematica 8, you could fit it to some statistical distribution. Now in Mathematica 9 you can use the exact same functions to fit it to a time series model or a differential equation, or whatever.
25 years ago, Mathematica didn’t put much emphasis on statistics. But over the years, we’ve steadily been building out extremely strong and often beyond-state-of-the-art statistical capabilities. And at this point, we’ve covered with great depth and robustness what’s needed for the vast majority of areas where statistical methods are used.
Of course, Mathematica is not an island. We’ve put a lot of emphasis on making sure that it can import and export an immense range of formats. And also that it can communicate with many external programs and systems. So in Mathematica 9, one thing we’ve added is built-in integration with the R statistics language. It’s pretty cool: I think it’s fair to say that it’s now easier to use R from within Mathematica than directly in the R system itself. So if there’s a package that’s been written in R for some specialized statistical task, you can immediately and seamlessly use it inside Mathematica.
Over the last few years, Mathematica has become a major player in the emerging field of data science. And to support that, we’ve been steadily expanding the types of data for which Mathematica has strong built-in support. We first added image processing in Mathematica 7, then enhanced it in Mathematica 8. Now in Mathematica 9, we’re making Mathematica’s already very complete image processing system do still more. There’s a convenient interactive Image Assistant, there’s feature tracking and face detection, there’s support for HDR and color profiles and there’s the ability to do out-of-core processing on very large images.
But probably the single most striking feature of image processing in Mathematica 9 is that it can handle not only 2D images, but also 3D volumetric ones. And in typical Mathematica style, most functions that work on 2D images now just seamlessly work on 3D images too. Beginning back in the early 1980s I used to try to use 3D volume rendering to visualize 3D cellular automata. And finally now what has always been elaborate and painful has become a Mathematica 9 one-liner that executes instantaneously. I’ve also over the years tried quite a few times to manipulate 3D DICOM-style data from MRIs and the like—and it’s always been quite challenging. But now in Mathematica 9 it’s become incredibly easy—and one’s immediately able not just to do visualization, but also to use all sorts of sophisticated analysis methods.

Another area that’s come of age in Mathematica 9 is signal processing—now with hundreds of functions for efficiently analyzing and filtering signals. It’s pretty impressive how smoothly it fits into Mathematica. Whether operating on a standard time-domain signal, or audio, or 2D or 3D images—and whether one’s doing visualization, applying continuous or discrete calculus, or doing high-precision or exact computations. And because Mathematica is a symbolic language, it’s immediately possible to represent filters for signal processing in a symbolic way—so they can be designed and manipulated with the full power of the Mathematica system, as well, for example, as being shared with Wolfram SystemModeler.
Mathematica 8 began the introduction of built-in control theory capabilities in Mathematica. Mathematica 9 fills this out, adding PID controllers, time delays and full support for descriptor systems. And of course, all this is fully integrated with signal processing, visualization and everything else in Mathematica, and Wolfram SystemModeler.
The list of new frontiers and new capabilities in Mathematica 9 is long. Two more that have been long in the making are built-in support for vector analysis and for symbolic tensors. In both cases, there have been deep challenges both in algorithms and in design. Indeed, for example, for more than 20 years I’ve been thinking about how to conveniently fit traditional vector analysis notation—with its often implicit reference to coordinate systems—into Mathematica. And it’s interesting that what it’s taken to solve this problem is in a sense a deeper understanding of just what coordinate systems really mean. But the result is that it’s now easy in Mathematica 9 to deal with symbolic vector expressions and with vector calculus in all standard named coordinate systems.
In working with symbolic tensors, I myself have a long history. Indeed, the first large-scale package that I ever wrote for symbolic computation—in 1978—dealt with symbolic tensors. But it’s taken until now for us to understand at the level needed for Mathematica just how really to work with them. A key problem is how to canonicalize products of tensors with contracted indices. I always suspected that there might be really powerful algorithms for this. And indeed there are, based on graph theory. And they’re now fully implemented in Mathematica 9. With the result that computations in general relativity that even recently seemed like major research projects now happen in mere seconds.
Looking down the complete list of what’s new in Mathematica 9, it’s pretty impressive. In addition to major new areas, there are countless extensions and enhancements throughout the system. Whether it’s responding to suggestions from math teachers to conveniently support real-valued cube roots. Or to allow giant data arrays limited only by 64-bit addressing. Or to support programmatic access to password-protected websites, synchronously or asynchronously. Or to support business dates in a streamlined way. Or to add elegantly designed interactive gauges to use in dashboard or for controls. Or to have a systematic framework for adding legends to any kind of plot. Or to make it possible to do enterprise-level distribution of CDF documents that make use of live data.
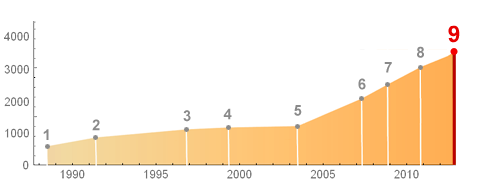
It’s been two years since we released Mathematica 8, and to me it’s very impressive how many new things have been finished in just those two years. Back with Mathematica 6, we built a framework that allowed us to start growing Mathematica at a much faster rate. And it’s interesting to see the effect of that in the plot below of the growth of the number of functions built into Mathematica. Today as we add higher and higher levels of automation to Mathematica, we are increasingly dealing with “superfunctions” that each cover larger and larger areas of functionality. But even so, we see that the dramatic growth in total number of functions has continued with Mathematica 9.
I’ve spent nearly half my life so far overseeing the design of Mathematica. And so for me it’s particularly interesting to see two major developments in Mathematica 9 that relate to design. The first is the increasing use of Wolfram|Alpha ideas and functionality in Mathematica, for example in the handling of units. And the second is the arrival of the Predictive Interface, which provides a new level of automation and discoverability in using Mathematica. Already in Mathematica 9 these are important directions. But I expect in the future they’ll give us the flexibility and the new ways of thinking that we need to unlock a whole sequence of spectacular possibilities.
One might think that after so many years and so many versions, it wouldn’t feel much different to be using Mathematica 9 compared to Mathematica 8. But it does. From the very beginning, whether it’s the new updated design, or the Predictive Interface, it’s very clear that Mathematica 9 is something fundamentally sleeker and stronger than anything that’s come before. And for me, what has happened with Mathematica 9—as with previous new versions of Mathematica—is that I quickly start being able to do more things, more quickly. Old programs that took many lines I can now replace with single, more general and easier-to-understand, Mathematica 9 functions. And things that I never got around to doing before I now do, because they’ve become so easy in Mathematica 9.
Being the kind of software company CEO that I am, I’m always using the latest test versions of all our products while they’re under development. But especially with Mathematica, it’s only close to the end that one can typically see the full vision of a new version emerge from all the threads of development that it involves. And so it has been with Mathematica 9. But what we have now is exciting, ground-breaking, and a great pleasure to use. And I am proud to be able to announce that as of today it is available to everyone.





