(This is the first of a series of posts related to next week’s tenth anniversary of A New Kind of Science. The second covers what’s happened since it was published, and the third its future.)
On May 14, 2012, it’ll be 10 years since A New Kind of Science (“the NKS book”) was published.
After 20 years of research, and nearly 11 years writing the book, I’d taken most things about as far as I could at that time. And so when the book was finished, I mainly launched myself back into technology development. And inspired by my work on the NKS book, I’m happy to say that I’ve had a very fruitful decade (Mathematica reinvented, CDF, Wolfram|Alpha, etc.).
I’ve been doing little bits of NKS-oriented science here and there (notably at our annual Summer School). But mostly I’ve been busy with other things. And so it’s been other people who’ve been having the fun of moving the science of NKS forward. But almost every day I’ll hear about something that’s been being done with NKS. And as we approach the 10-year mark, I’ve been very curious to try to get at least a slightly more systematic view of what’s been going on.
A place to start is the academic literature, where there’s now an average of slightly over one new paper per day published citing the NKS book—with that number steadily increasing. The papers span all kinds of areas (here identified by journal fields):

And looking through the list of papers my main response is “Wow—so much stuff”. Some of the early papers seem a bit questionable, but as the decade has gone on, my impression from skimming through papers is that people are really “getting it”—understanding the ideas in the NKS book, and making good and interesting use of them.
There are typically three broad categories of NKS work: pure NKS, applied NKS, and the NKS way of thinking.
Pure NKS is about studying the computational universe as basic science for its own sake—investigating simple programs like cellular automata, seeing what they do, and gradually abstracting general principles. Applied NKS is about taking what one finds in the computational universe, and using it as raw material to create models, technology and other things. And the NKS way of thinking is about taking ideas and principles from NKS—like computational irreducibility or the Principle of Computational Equivalence—and using them as a conceptual framework for thinking about things.
And with these categories, here’s how the academic papers published in different types of journals break down:

So what are all these papers actually about? Let’s start with the largest group: applied NKS. And among these, a striking feature is the development of models for a dizzying array of systems and phenomena. In traditional science, new models are fairly rare. But in just a decade of applied NKS academic literature, there are already hundreds of new models.
Hair patterns in mice. Shapes of human molars. Collective butterfly motion. Evolution of soil thicknesses. Interactions of trading strategies. Clustering of red blood cells in capillaries. Patterns of worm appendages. Shapes of galaxies. Effects of fires on ecosystems. Structure of stromatolites. Patterns of leaf stomata operation. Spatial spread of influenza in hospitals. Pedestrian traffic flow. Skin cancer development. Size distributions of companies. Microscopic origins of friction. And many, many more.
One of the key lessons of NKS is that even when a phenomenon appears complex, there may still be a simple underlying model for it. And to me one of the most interesting features of the applied NKS literature is that over the course of the decade typical successful models have been getting simpler and simpler—presumably as people get more confident in using the methods and ideas of NKS.
Of NKS-based models now in use, the vast majority are still based on cellular automata—the very first simple programs I studied back in the early 1980s. There’s been some use of substitution systems, mobile automata and various graph-based systems. But cellular automata are still definitely the leaders. And beginning with my work on them in the early 1980s, there’s been steady growth in their use for nearly 30 years. (Notably, the numbers of papers about them firmly overtook the number of papers about Turing machines around 1995.)

It’s notable that the breakdown of cellular automaton papers is distinctly different from the breakdown of all NKS papers:

And it’s a great testament to the importance of simple rules that even among the 256 simplest possible cellular automata, there’ve now been papers written about almost every single one of them. (The top rules, which also happen to be top in the NKS book, are rule 110, rule 30 and rule 90—which respectively show provable computation universality, high-quality randomness generation and additive nested structure capable of mathematical analysis).
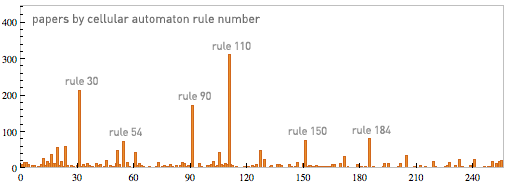
Many of these papers are applied NKS, using cellular automata as models (rule 184 for traffic flow, rule 90 for catalysis, rule 54 for phase transitions, etc.). But many are also pure NKS, studying the cellular automata for their own sake.
In a sense, each possible cellular automaton rule is a world unto itself. And over the course of the past decade, a whole variety of pockets of literature have developed around specific rules—typically using various computational and mathematical methods to identify and prove features of their behavior (nesting in the boundary of rule 30, blocks in rule 146, logic structures in rule 54, etc.) And in general, it continues to amaze me just how many things are still being discovered even about the very simplest possible cellular automaton rules—that I first studied 30 years ago.
One of my favorite activities when I worked on the NKS book was just to go out into the computational universe, and explore what’s there. In a sense it’s like quintessential natural science—but now concerned with exploring not stars and galaxies or biological flora and fauna, but instead abstract programs. Over the years I’ve developed a whole methodology for exploring the computational universe, and for doing computer experiments. And it’s interesting to see the gradual spread of this methodology—rather obviously visible, for example, in all sorts of papers with pictures that look as if they could have come straight from the NKS book. (Most often, there are arrays of black-and-white rasters and the like; the more elaborate style of algorithmic diagrams in the NKS book are still much rarer—even though recent versions of Mathematica have made them easier to make.)
There’s been an issue, though, in that raw explorations of the computational universe don’t fit terribly well into current patterns of academia and academic publishing. We’ve tried to do what we can with our Complex Systems journal (published since 1986), but ultimately there are new venues and models needed, based more on structured knowledge and less on academic narrative. Soon after the NKS book came out, we did some experiments on developing an “Atlas of Simple Programs”—but we realized that to make this truly useful, we’d need something not so much like an atlas, but more like a computational knowledge engine. And of course, now with Wolfram|Alpha we have just that—and we’re gradually adding lots of NKS knowledge to it:
If one looks at pure NKS work over the past decade, the vast majority has been concerned with types of systems that I already discussed in some form or another in the book. Cellular automata remain the most common, but there are also recursive sequences, substitution systems, network systems, tag systems, and all sorts of others. And there’ve been some significant generalizations, and some new kinds of systems. Cellular automata with non-local rules, with memory, or on networks. Turing machines with skips. Iterated finite automata. Distance transform automata. Planar trinets. Generalized reversal-addition systems. And others.
Much of the systematic work that’s been done on pure NKS has been by “professional scientists” who publish in traditional academic journals. But some of the most interesting and innovative work has actually been done by amateurs (most often people involved in some facet of the computer industry) who have the advantage of not having to follow the constraints of academic publishing—but at least for now have the disadvantage that there is no centralized venue for their contributions.
In pure NKS, one often starts from raw observations of the computational universe, but then moves on to detailed analysis, and to the formulation of increasingly general principles. And in the past 10 years all sorts of analyses have been done. Classification of compressibility of outputs from simple programs. Possible forms of boundaries for cellular automaton growth. Empirical analysis of Turing machine running times. Sequences of possible periods in cellular automata. Symmetries of finite Turing machine state transition diagrams. Universal algebra properties of cellular automata. And lots more.
Needless to say, there are still plenty of things that remain far out of reach—like proving any significant degree of randomness for sequences generated by rule 30. But in 2007, to celebrate the fifth anniversary of the publication of the NKS book, I decided to issue a challenge—and offered a $25,000 prize for determining whether or not a particular simple Turing machine from the book is computation universal. I thought this challenge might remain open for a century—but I was thrilled when after just a few months, it was answered in the affirmative by a young English computer science student.
Not only did this establish the identity of the very simplest universal Turing machine—but it also provided an important new piece of evidence for what I consider to be the most powerful principle to emerge so far in pure NKS: the Principle of Computational Equivalence.
In academic work on pure NKS, there’s been a definite strand of attempts to further formalize concepts and principles in the book—and perhaps prove or disprove them—most often using methods from mathematical logic or theoretical computer science. The four classes of cellular automaton behavior. The Principle of Computational Equivalence. Computational irreducibility. Intrinsic randomness. Over the past decade all sorts of results for particular simplified versions or situations have been obtained—but in the absence of major new methods, nothing complete or definitive has emerged.
Beyond pure and applied NKS, another important component of the NKS academic literature is work based on the NKS way of thinking. Quite often NKS has been used in connection with questions about the methodology of science and the foundations of modeling. But there’s also all sorts of use of NKS in thinking about mainstream issues in fields like philosophy, social science, theology, economics, psychology, politics, law and management science.
My impression is that some important things are happening here. It’s taken a long time for the traditional mathematical approach to science to be applied at all to these areas. And in many cases it’s not been terribly helpful. But with the NKS way of thinking there’s a whole new way that ideas from science can enter. Which seems both to clarify many longstanding issues, and to make it possible to discuss all sorts of new ones.
Free will in philosophy. Possible organizational structures in management science. Theoretical controllability in economics. Liability for consequences in law. There are surprisingly definite things that have been said about all these on the basis of NKS ideas.
One of the things that’s happened over the decade since the NKS book was published is the development of countless fields that go by the name “computational ___”. There’s computational philosophy, computational history, computational social science, computational law—and many others.
And perhaps one of the most important uses of NKS and the NKS way of thinking is that it provides a core intellectual foundation for these fields. There’s usually an important level at which one’s dealing mainly with practical computation (often using Mathematica). But when one’s concerned with foundational theoretical principles, NKS very often seems to be the key. And as one traces the expansion of these new fields, one can see rather clearly in the academic literature a corresponding spreading of NKS ideas.
But in the effort to get a global view of the progress of NKS, the academic literature is just one part of the story.
There’s also all sorts of very diverse discussion of NKS ideas in blogs, news commentaries, opinion pieces and the like. Sometimes NKS is used to bolster or attack some political argument or another. Sometimes NKS is invoked just to show that there are new and different ideas to consider. And sometimes NKS is used in ways where it’s hard (at least for me) to tell if it makes sense (relations to Eastern religious traditions, unusual sensory experiences, etc.).
It’s been fun over the past decade to watch NKS gradually make its way into popular culture. Whether it’s in cartoon strips that pithily use some NKS idea. Or in fiction that uses NKS to theme some character. Or whether it’s a cameo appearance of the physical NKS book—or an NKS piece of dialog—on a TV show.
There’ve been quite a few science fiction novels where NKS has been central. Sometimes there’s a hero or villain who pursues NKS research or ideas. Sometimes NKS enters in the understanding of what a future governed by computation would be like. And sometimes there’s some object whose operation or purpose can only be understood in NKS terms.
In a rather different direction, another major use of NKS has been in art.
From my very earliest investigations of cellular automata, we’ve known that they can create rich and aesthetically pleasing visual images. But the publication of the NKS book dramatically accelerated the use of systems like cellular automata for artistic purposes. And in the past decade I’ve seen cellular automaton patterns artistically rendered in paint, knitting, mosaic, sticks, cake decoration, punched holes, wood blocks, smoke, water valves and no doubt all sorts of other media that I can’t immediately even imagine.

In the interactive domain, there are countless websites and apps that run cellular automata and other NKS systems. Sometimes what’s done is a fairly straightforward rendering of the underlying system—not unlike what’s in the NKS book. And sometimes there is extensive artistic interpretation done. Sometimes what’s built is used essentially for hobbyist NKS explorations, sometimes for art, and sometimes for pure entertainment.
In games—and movies—NKS systems have been extensively used both to produce detailed effects such as textures, and to handle for example collective behavior of large numbers of similar entities. NKS systems are also used to define overall rules for games or for characters in games.
NKS is not limited to visual form. And indeed NKS systems have been used extensively to generate audio—with probably the most ambitious experiment in this direction being our 2005 WolframTones project.
Of all responses to the NKS book, one of the consistently strongest has been from the architecture community. Many times I have heard how much architects value both the physical book and its illustrations, as well as the ideas about creation of form that it contains.
I don’t know if there’s any large actual building yet constructed from the simple rules of an NKS system. But I know quite a few have been planned. And there’s also been significant work done on landscape architecture and urban planning—not to mention interior design—with NKS systems.
There’ve been many important applications of NKS in the sciences, humanities and arts over the past decade. But if there’s one area where the effect of NKS has been emerging as most significant, it’s technology. Just as the computational universe gives us an inexhaustible supply of new models, so also it gives us an inexhaustible supply of new mechanisms that we can harness for technology. And indeed in our own technology development over the past decade, we have made increasing use of NKS.
A typical pattern is that we identify some task, and then we search the computational universe for a simple program to carry out the task. Often this kind of mining of the computational universe seems like magic—and the programs we discover seem much cleverer than anything we would have ever come up with by our usual engineering methods of step-by-step construction.
Years ago we started using rule 30 as the pseudorandom generator in Mathematica—and more recently we’ve done large-scale search to find other cellular automata that are slightly more efficient for this task. Over the years we’ve also mined the computational universe to find efficient hash codes, function evaluation algorithms, image filters, linguistics algorithms, visual layout methods and much, much more. Sometimes there’s something known from pure NKS that immediately suggests some particular rule or type of system to use; more often we need to do a systematic search from scratch.
It’s a little hard to track how NKS has been used in technology in the world at large. There are a handful of patents that refer to NKS, and a number of organizations have systematically sought my advice about using NKS—but most of what I’ve heard about technology uses of NKS has come from anecdotes and chance encounters.
Sometimes it’s at least somewhat clear on the surface, because there’s some visible NKS-like pattern to be seen—say in window shade arrangements for buildings, antenna designs, contact lens patterns, heat conduction networks, and so on.
But more often it’s a case of “NKS inside”, where there’s some internal algorithm that’s been found by exploring the computational universe. By now I know of a large number of examples. Modular robots. Mesh networks. Cryptography. Image processing. Network routing. Computer security. Concurrency protocols. Computer graphics. Algorithmic texture generation. Probabilistic processor designs. Games. Traffic light control. Voting schemes. Financial trading systems. Precursors to algorithmic drugs. And many more.
It’s not like the academic literature, where (at least in theory) there are citations to be followed. But my strong impression is that the use of NKS in practical technology is starting to dwarf its use in basic research. In part this is just a sign of healthy development in the direction of applications.
But in part it is, I think, also a reflection of limitations in the current structure of academia and basic research. For university departments and research funding programs are typically organized according to disciplines that are many decades old—and are ill equipped to adapt to new directions like NKS that do not fit into their existing structures.
Still, over the past decade, there have sprung up around the world a good number of groups that are successfully carrying out basic NKS research. The story in each case is different. Particular leadership; special reasons for institutional or government support; particular ways to survive “interstitially” in an institution; and so on. But gradually more and more of these pockets are developing, and prospering.
When the NKS book appeared, I visited many universities and research labs—and talked to many university presidents, lab directors, and the like. A common response was excitement not only about the subject matter of NKS, but also about the social phenomenon that at talks and lunches about NKS, people who might have been in different parts of an institution for decades were actually meeting—and interacting—in ways they’d never done before.
For a while I thought it might make sense to use this enthusiasm to help launch strong NKS initiatives at particular existing institutions. But after some investigation, it became clear that this was not going to be any kind of quick process. It wasn’t like at our company, where a significant new initiative can be launched in days. This was something that was going to take years—if not decades—to achieve.
And actually, I pretty much knew what to expect. Because I’d seen something very similar before. Back in the early 1980s, after I made my first discoveries about cellular automata, I realized that studying complex systems with simple rules was going to be an important area. And so I set about developing and promoting what I called “complex systems research” (I avoided the eventually-more-common term “complexity theory” out of a deference to the existing area of theoretical computer science by that name).
I soon started the first research center in the field (the Center for Complex Systems Research at the University of Illinois), and the first journal (Complex Systems). I encouraged the then-embryonic Santa Fe Institute to get into the field (which they did), and did my best to expand support for the field. But things went far too slowly for me—and in 1986 I decided that a better personal strategy would be to build the best possible tools I could (Mathematica), get the best possible personal environment (Wolfram Research), and then have the fun of doing the research myself. And indeed this is how I came to embark on A New Kind of Science, and ultimately to take things in a rather different direction.
So what happened to complexity? Here’s a plot of the number of “complexity institutes” in the world by founding date (at least the ones we could find):

And here’s their current geographic distribution (some excellent ones are doubtless missing!):

(Fully half of all complexity institutes we identified didn’t tell us their founding dates. The institutes in operation before 1986 were originally rather different from what I called complex systems research, but have evolved to be much closer.)
So what does this tell us? The main thing as far as I’m concerned is that the development of institutions is slow and inexorable. Until we collected the data I had no idea there were now so many complexity institutes in the world. But it took close to three decades to get to this point. I think NKS is off to a quicker start. But it’s not clear what one does to accelerate it, and it’s still inevitably going to take a long time.
I might say that I think the intellectual development of NKS is going much better than it ever did for complexity. Because for NKS there’s a core of pure NKS—as well as the NKS way of thinking—that’s successfully being studied, and building up a larger and larger body of definite formal knowledge. In complexity, however, there was an almost immediate fragmentation into lots of different—and often somewhat questionable—application areas. Insofar as these applications followed traditional disciplinary lines, it was often easier to get institutional support for them. But with almost no emphasis on any kind of core intellectual structure, it’s been difficult for coherent progress to be made.
What’s exciting to see with NKS is that in addition to strong applications—especially in technology—there is serious investment in general abstract core development. Which means that independent of success in any particular application area, there’s a whole intellectual structure that’s growing. And such structures—like for example pure mathematics—have tended to have implications of great breadth, historically spanning millennia.
So how should people find out about NKS? Well, I put all the effort I did into writing A New Kind of Science to make that as easy as possible for as broad a range of people as possible. And I think that for the most part that worked out very well. Indeed, it’s been remarkable over the past decade how many people I’ve run into—often in unexpected places—who seem to have read and absorbed the contents of the NKS book.
And to me what’s been most interesting is how many different walks of life those people come from. Occasionally they’re academics, with specific interests. More often they’re other kinds of intellectually oriented people. Sometimes they’re involved with computers; sometimes they’re not. Sometimes they’re highly educated; sometimes they’re not. Sometimes they’re young; sometimes they’re old. And occasionally they turn out to be famous—often for things that at first seem to have no connection to interest in NKS.
I suppose for me one of the most satisfying things about the spread of NKS is seeing people get so much pleasure out of taking on the serious pursuit of NKS. I have a theory that for almost everyone there is a certain direction that’s really their ideal niche. Too often people go through their lives without finding it. Or they live at a time in history when it simply does not exist. But when something like NKS comes along, there’s a certain set of people for whom this is their thing: this is the direction that really fits them. I’m of course an example, and I feel very fortunate to have found NKS. But what’s been wonderful over the past decade is to see all sorts of other people—at different stages in their lives—having that experience too.
There’s much to do in spreading knowledge about NKS. I started the job with the NKS book. But by now NKS has found its way into plenty of textbooks and popular books. Our Demonstrations Project has lots of interactive demonstrations of NKS concepts. And there are other apps and websites too.
For me a major effort in NKS education has been our Summer School, held every year since 2003. We’ve had a diverse collection of outstanding students, and it’s been invigorating each year to see the variety of NKS projects that they’ve been able to pursue. But I suppose if there’s been one discovery for me from the Summer School, it’s been what an important general educational foundation NKS provides.
One can study NKS for its own sake, just as one can study math or physics for their own sake. But like math or physics, one can also study NKS as a way to develop general patterns of thinking to apply all over the place. This works at the level of education for business executives—and it also works at much lower educational levels.
When I first saw people suggesting that young kids work out cellular automaton evolutions by hand on graph paper, I thought it was a little nutty. But then I realized that it’s a great exercise in precision work, with rather satisfying results, that also teaches a kind of “pre-computer-science” idea of what algorithms are. Oh, and it can also be quite aesthetic, and even has direct connections with nature (yes, teachers ask us where to get patterned mollusc shells).
There have now been many courses at graduate, undergraduate and high school levels that use the NKS book. And while I don’t know everything that’s happened, I know that there have at least been experiments with NKS at middle school and elementary school levels.
For me, one of the interesting things is that it’s so easy for anyone to discover something original in NKS. At the beginning of our Summer School we always ask each student to find an “interesting” cellular automaton—and they inevitably come back with a rule that has never been seen before. The computational universe is so vast—and still so unexplored—that anyone can find their own part of it. And then it’s a question of having a good methodology and being systematic to be able to discover something of real value.
When I look at the NKS book now, I’m pleased how well it has withstood the past 10 years. New things have been discovered, but they do not supersede what’s in the book. And even with all the scrutiny and detailed study the book has received, not a single significant error has surfaced. And the pictures are direct and abstract enough to be in a sense timeless (much like a Platonic solid from ancient Egypt looks the same as one today). Of course, while the paper version of the book is elegant and classic—and seems to me a little ceremonial—the book is now much more read on the web and the iPad.
But what of the detailed content of the book? There are certainly plenty of academic papers that cite specific pages of the book. But as I look through the book, I cannot help but be struck by how much more there is to “mine” from it. In writing the book—with Mathematica at my side—it felt as if I had developed a kind of industrial-scale way of making discoveries. Thousands of them. That I discussed in the main part of the book, or put in tiny print and little diagrams into the notes at the back.
It’s been interesting to see what’s been absorbed, at what rate. Different fields seem to have different characteristic times. Art, for example, is very fast. Within months after the NKS book came out, there was significant activity among artists based on NKS concepts. No doubt because in art there’s always excitement about the new.
The same was true for example in finance and trading. Where again there is a great premium for the new.
But in other fields, things were slower. The younger and more entrepreneurial the field, the faster things seemed to go. And the less set the conceptual framework for the field, the deeper the early absorption would be. In fields like mathematics and physics where there’s a tradition of precise results, some basic technical understanding came quickly. But in these old and mature fields, the rate of real absorption seemed to be incredibly slow. And indeed, if I look at what I consider major gaps in the follow-up to the NKS book, they are centered around mathematics and physics—with a notable area being the work on the fundamental theory of physics in the book.
In a sense, ten years is a short time for the kind of development that I believe NKS represents. Indeed, in my own life so far, I have found that ten years is about the minimum time it takes me to really begin to come to terms with new frameworks for thinking about things. And certainly in the general history of science and of ideas, ten years is no time at all. Indeed, ten years after the publication of Newton’s Principia, for example, almost none of the people who would make the next major advances had even been born yet.
And ten years after the publication of A New Kind of Science, I am personally quite satisfied with what I can see of the development of the field. Certainly there is far to go, but a solid start has been made, many important steps have been taken, and the inexorable progress of NKS seems assured.







