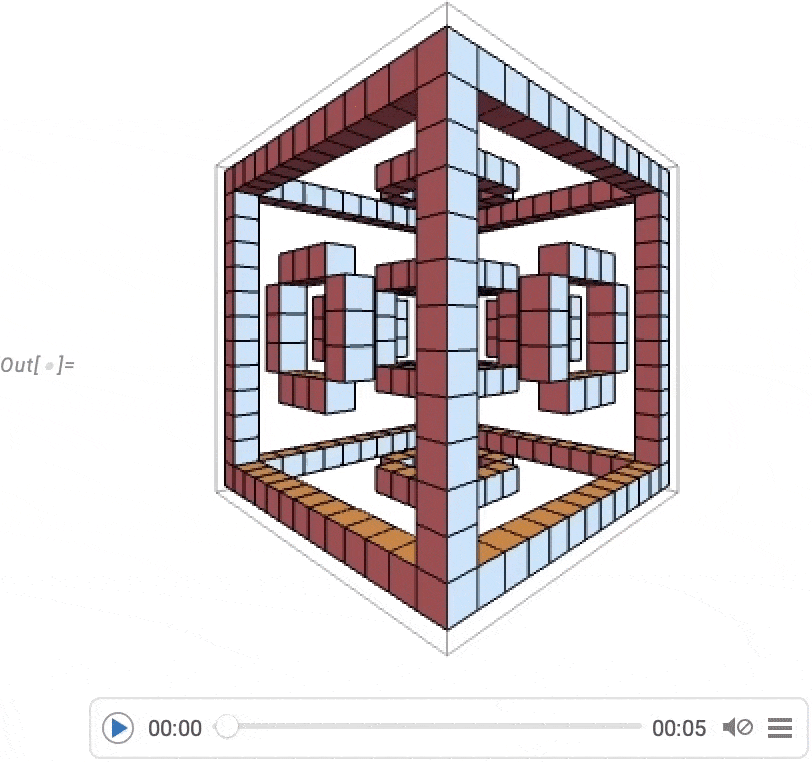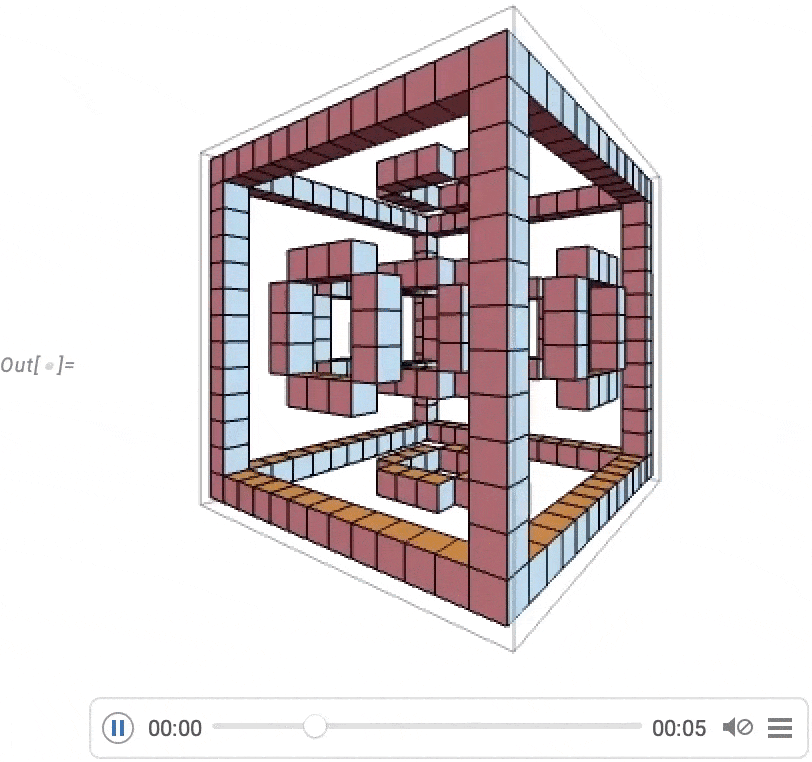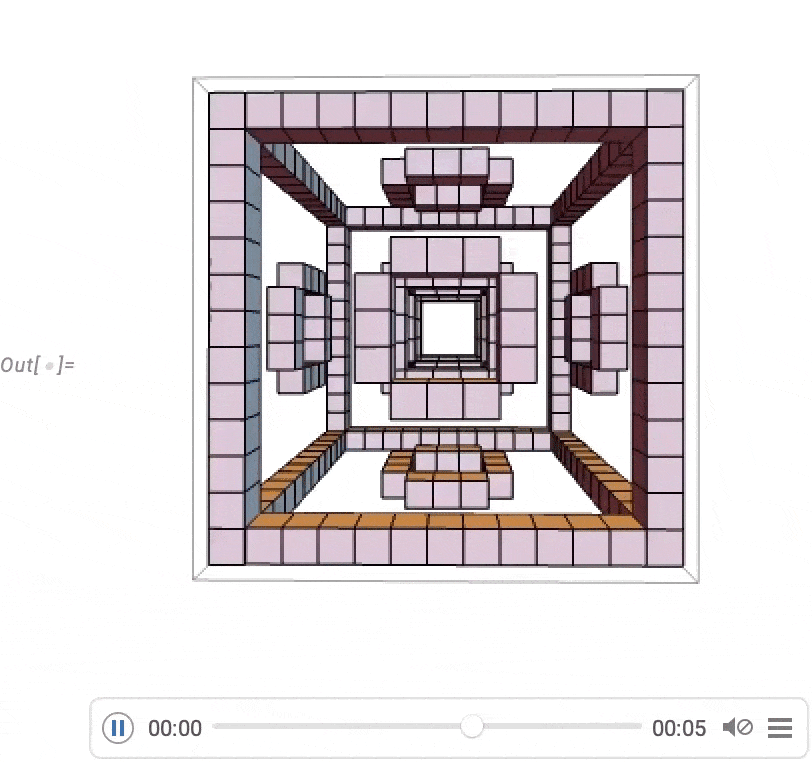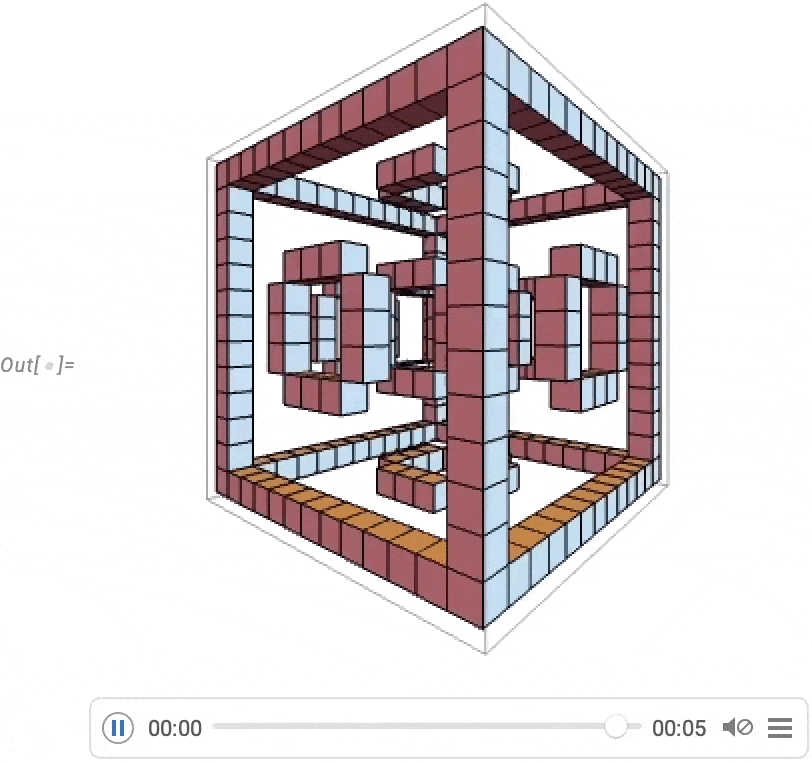
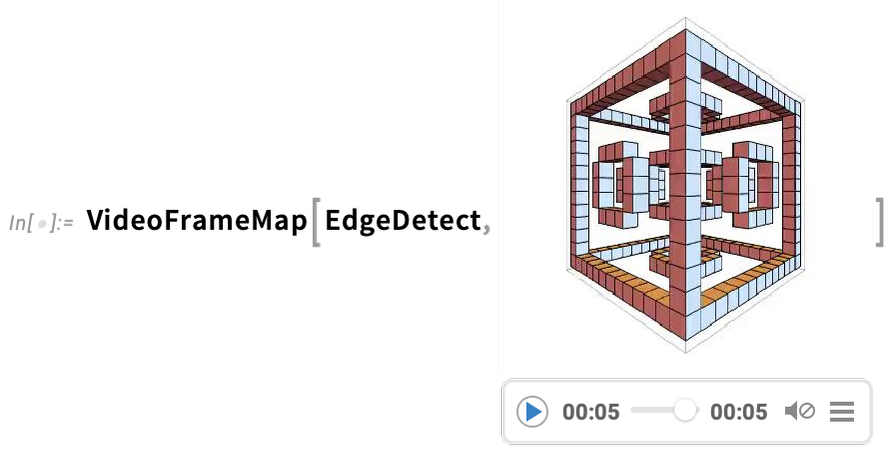
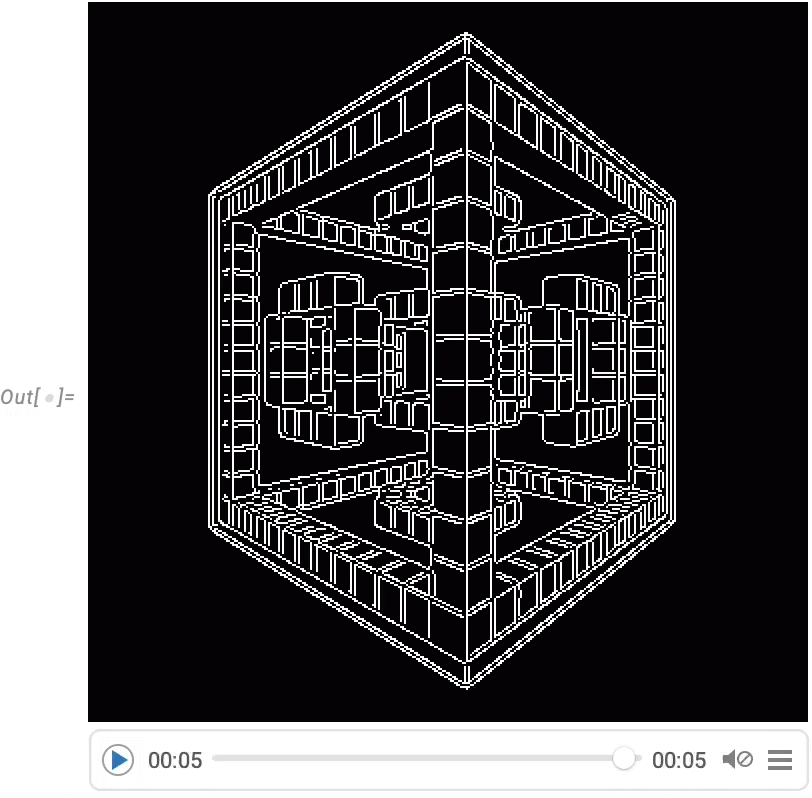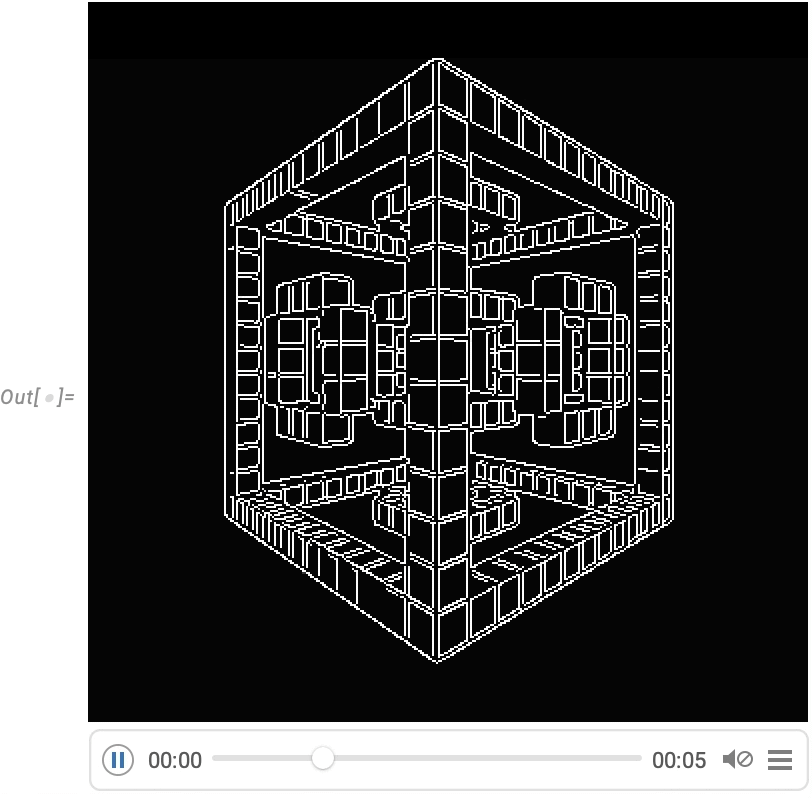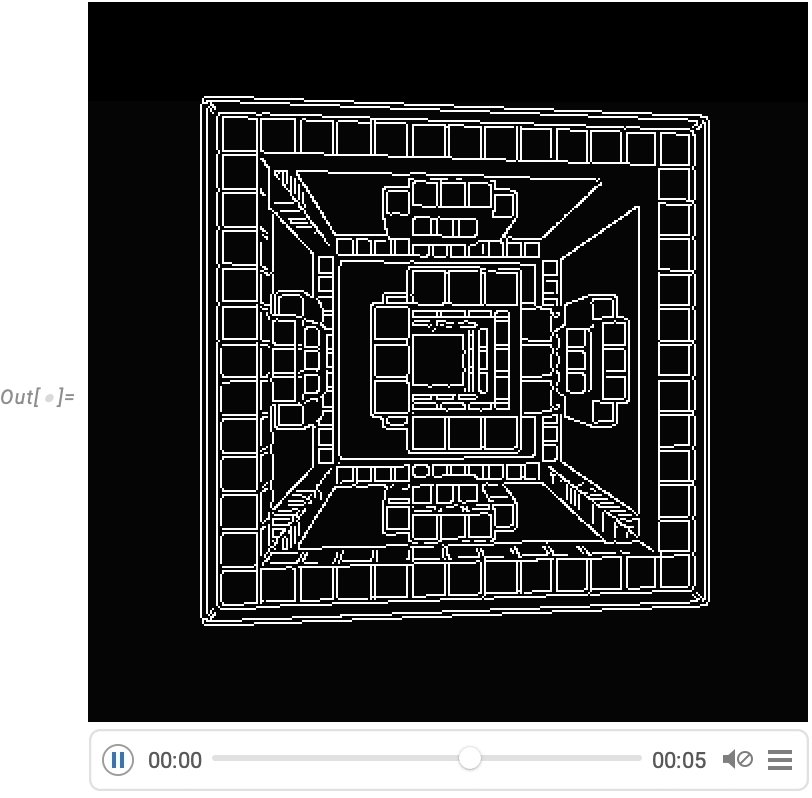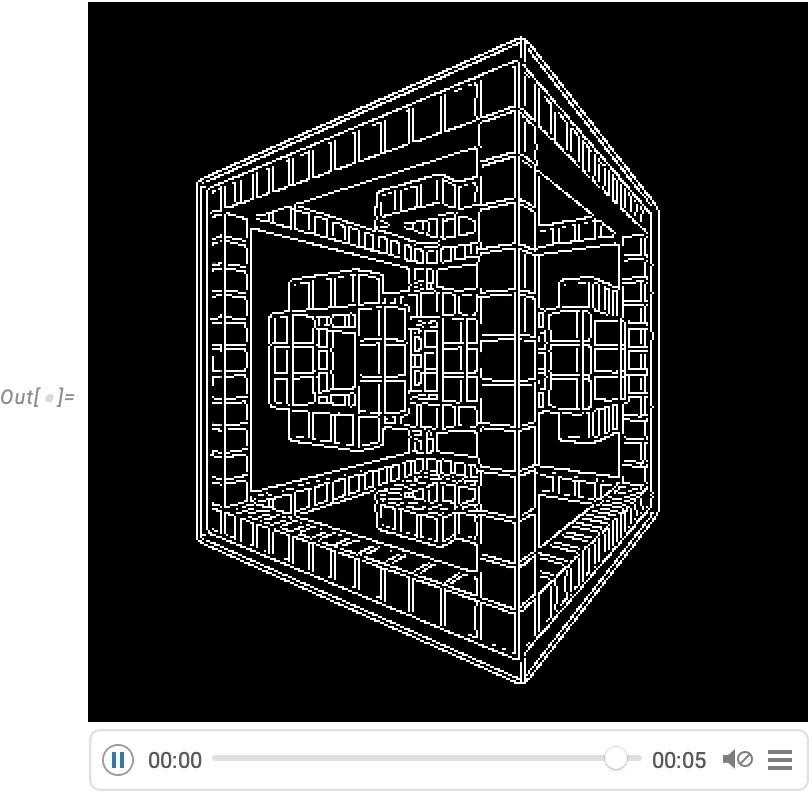
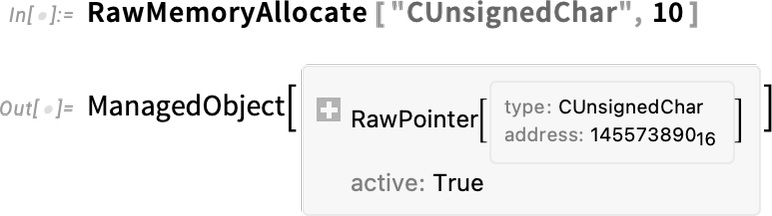
Note: Click any diagram to get Wolfram Language code to reproduce it. Wolfram Language code for training the neural nets used here is also available (requires GPU).

Won’t AI Eventually Be Able to Do Everything?
Particularly given its recent surprise successes, there’s a somewhat widespread belief that eventually AI will be able to “do everything”, or at least everything we currently do. So what about science? Over the centuries we humans have made incremental progress, gradually building up what’s now essentially the single largest intellectual edifice of our civilization. But despite all our efforts, there are still all sorts of scientific questions that remain. So can AI now come in and just solve all of them?
To this ultimate question we’re going to see that the answer is inevitably and firmly no. But that certainly doesn’t mean AI can’t importantly help the progress of science. At a very practical level, for example, LLMs provide a new kind of linguistic interface to the computational capabilities that we’ve spent so long building in the Wolfram Language. And through their knowledge of “conventional scientific wisdom” LLMs can often provide what amounts to very high-level “autocomplete” for filling in “conventional answers” or “conventional next steps” in scientific work.
But what I want to do here is to discuss what amount to deeper questions about AI in science. Three centuries ago science was transformed by the idea of representing the world using mathematics. And in our times we’re in the middle of a major transformation to a fundamentally computational representation of the world (and, yes, that’s what our Wolfram Language computational language is all about). So how does AI stack up? Should we think of it essentially as a practical tool for accessing existing methods, or does it provide something fundamentally new for science?
My goal here is to explore and assess what AI can and can’t be expected to do in science. I’m going to consider a number of specific examples, simplified to bring out the essence of what is (or isn’t) going on. I’m going to talk about intuition and expectations based on what we’ve seen so far. And I’m going to discuss some of the theoretical—and in some ways philosophical—underpinnings of what’s possible and what’s not.
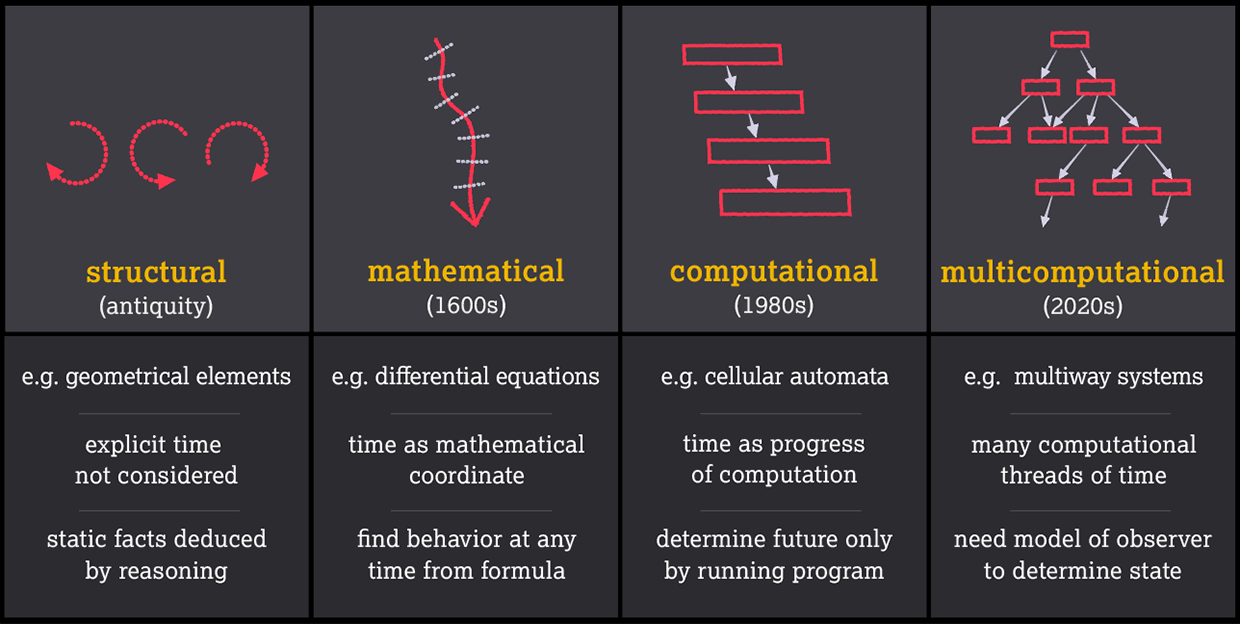
So what do I actually even mean by “AI” here? In the past, anything seriously computational was often considered “AI”, in which case, for example, what we’ve done for so long with our Wolfram Language computational language would qualify—as would all my “ruliological” study of simple programs in the computational universe. But here for the most part I’m going to adopt a narrower definition—and say that AI is something based on machine learning (and usually implemented with neural networks), that’s been incrementally trained from examples it’s been given. Often I’ll add another piece as well: that those examples include either a large corpus of human-generated scientific text, etc., or a corpus of actual experience about things that happen in the world—or, in other words, that in addition to being a “raw learning machine” the AI is something that’s already learned from lots of human-aligned knowledge.
OK, so we’ve said what we mean by AI. So now what do we mean by science, and by “doing science”? Ultimately it’s all about taking things that are “out there in the world” (and usually the natural world) and having ways to connect or translate them to things we can think or reason about. But there are several, rather different, common “workflows” for actually doing science. Some center around prediction: given observed behavior, predict what will happen; find a model that we can explicitly state that says how a system will behave; given an existing theory, determine its specific implications. Other workflows are more about explanation: given a behavior, produce a human-understandable narrative for it; find analogies between different systems or models. And still other workflows are more about creating things: discover something that has particular properties; discover something “interesting”.
In what follows we’ll explore these workflows in more detail, seeing how they can (or cannot) be transformed—or informed—by AI. But before we get into this, we need to discuss something that looms over any attempt to “solve science”: the phenomenon of computational irreducibility.
The Hard Limit of Computational Irreducibility
Often in doing science there’s a big challenge in finding the underlying rules by which some system operates. But let’s say we’ve found those rules, and we’ve got some formal way to represent them, say as a program. Then there’s still a question of what those rules imply for the actual behavior of the system. Yes, we can explicitly apply the rules step by step and trace what happens. But can we—in one fell swoop—just “solve everything” and know how the system will behave?
To do that, we in a sense have to be “infinitely smarter” than the system. The system has to go through all those steps—but somehow we can “jump ahead” and immediately figure out the outcome. A key idea—ultimately supported at a foundational level by our Physics Project—is that we can think of everything that happens as a computational process. The system is doing a computation to determine its behavior. We humans—or, for that matter, any AIs we create—also have to do computations to try to predict or “solve” that behavior. But the Principle of Computational Equivalence says that these computations are all at most equivalent in their sophistication. And this means that we can’t expect to systematically “jump ahead” and predict or “solve” the system; it inevitably takes a certain irreducible amount of computational work to figure out what exactly the system will do. And so, try as we might, with AI or otherwise, we’ll ultimately be limited in our “scientific power” by the computational irreducibility of the behavior.
But given computational irreducibility, why is science actually possible at all? The key fact is that whenever there’s overall computational irreducibility, there are also an infinite number of pockets of computational reducibility. In other words, there are always certain aspects of a system about which things can be said using limited computational effort. And these are what we typically concentrate on in “doing science”.
But inevitably there are limits to this—and issues that run into computational irreducibility. Sometimes these manifest as questions we just can’t answer, and sometimes as “surprises” we couldn’t see coming. But the point is that if we want to “solve everything” we’ll inevitably be confronted with computational irreducibility, and there just won’t be any way—with AI or otherwise—to shortcut just simulating the system step by step.
There is, however, a subtlety here. What if all we ever want to know about are things that align with computational reducibility? A lot of science—and technology—has been constructed specifically around computationally reducible phenomena. And that’s for example why things like mathematical formulas have been able to be as successful in science as they have.
But we certainly know we haven’t yet solved everything we want in science. And in many cases it seems like we don’t really have a choice about what we need to study; nature, for example, forces it upon us. And the result is that we inevitably end up face-to-face with computational irreducibility.
As we’ll discuss, AI has the potential to give us streamlined ways to find certain kinds of pockets of computational reducibility. But there’ll always be computational irreducibility around, leading to unexpected “surprises” and things we just can’t quickly or “narratively” get to. Will this ever end? No. There’ll always be “more to discover”. Things that need more computation to reach. Pockets of computational reducibility that we didn’t know were there. And ultimately—AI or not—computational irreducibility is what will prevent us from ever being able to completely “solve science”.
There’s a curious historical resonance to all this. Back at the beginning of the twentieth century, there was a big question of whether all of mathematics could be “mechanically solved”. The arrival of Gödel’s theorem, however, seemed to establish that it could not. And now that we know that science also ultimately has a computational structure, the phenomenon of computational irreducibility—which is, in effect, a sharpening of Gödel’s theorem—shows that it too cannot be “mechanically solved”.
We can still ask, though, whether the mathematics—or science—that humans choose to study might manage to live solely in pockets of computational reducibility. But in a sense the ultimate reason that “math is hard” is that we’re constantly seeing evidence of computational irreducibility: we can’t get around actually having to compute things. Which is, for example, not what methods like neural net AI (at least without the help of tools like Wolfram Language) are good at.
Things That Have Worked in the Past
Before getting into the details of what modern machine-learning-based AI might be able to do in “solving science”, it seems worthwhile to recall some of what’s worked in the past—not least as a kind of baseline for what modern AI might now be able to add.
I myself have been using computers and computation to discover things in science for more than four decades now. My first big success came in 1981 when I decided to try enumerating all possible rules of a certain kind (elementary cellular automata) and then ran them on a computer to see what they did:
I’d assumed that with simple underlying rules, the final behavior would be correspondingly simple. But in a sense the computer didn’t assume that: it just enumerated rules and computed results. And so even though I never imagined it would be there, it was able to “discover” something like rule 30.
Over and over again I have had similar experiences: I can’t see how some system can manage to do anything “interesting”. But when I systematically enumerate possibilities, there it is: something unexpected, interesting—and “clever”—effectively discovered by computer.
In the early 1990s I wondered what the simplest possible universal Turing machine might be. I would never have been able to figure it out myself. The machine that had held the record since the early 1960s had 7 states and 4 colors. But the computer let me discover just by systematic enumeration the 2-state, 3-color machine
that in 2007 was proved universal (and, yes, it’s the simplest possible universal Turing machine).
In 2000 I was interested in what the simplest possible axiom system for logic (Boolean algebra) might be. The simplest known up to that time involved 9 binary (Nand) operations. But by systematically enumerating possibilities, I ended up finding the single 6-operation axiom  (which I proved correct using automated theorem proving). Once again, I had no idea this was “out there”, and certainly I would never have been able to construct it myself. But just by systematic enumeration the computer was able to find what seemed to me like a very “creative” result.
(which I proved correct using automated theorem proving). Once again, I had no idea this was “out there”, and certainly I would never have been able to construct it myself. But just by systematic enumeration the computer was able to find what seemed to me like a very “creative” result.
In 2019 I was doing another systematic enumeration, now of possible hypergraph rewriting rules that might correspond to the lowest-level structure of our physical universe. When I looked at the geometries that were generated I felt like as a human I could roughly classify what I saw. But were there outliers? I turned to something closer to “modern AI” to do the science—making a feature space plot of visual images:

It needed me as a human to interpret it, but, yes, there were outliers that had effectively been “automatically discovered” by the neural net that was making the feature space plot.
I’ll give one more example—of a rather different kind—from my personal experience. Back in 1987—as part of building Version 1.0 of what’s now Wolfram Language—we were trying to develop algorithms to compute hundreds of mathematical special functions over very broad ranges of arguments. In the past, people had painstakingly computed series approximations for specific cases. But our approach was to use what amounts to machine learning, burning months of computer time fitting parameters in rational approximations. Nowadays we might do something similar with neural nets rather than rational approximations. But in both cases the concept is to find a general model of the “world” one’s dealing with (here, values of special functions)—and try to learn the parameters in the model from actual data. It’s not exactly “solving science”, and it wouldn’t even allow one to “discover the unexpected”. But it’s a place where “AI-like” knowledge of general expectations about smoothness or simplicity lets one construct the analog of a scientific model.
Can AI Predict What Will Happen?
It’s not the only role of science—and in the sections that follow we’ll explore others. But historically what’s often been viewed as a defining feature of successful science is: can it predict what will happen? So now we can ask: does AI give us a dramatically better way to do this?
In the simplest case we basically want to use AI to do inductive inference. We feed in the results of a bunch of measurements, then ask the AI to predict the results of measurements we haven’t yet done. At this level, we’re treating the AI as a black box; it doesn’t matter what’s happening inside; all we care about is whether the AI gives us the right answer. We might think that somehow we can set up the AI up so that it “isn’t making any assumptions”—and is just “following the data”. But it’s inevitable that there’ll be some underlying structure in the AI, that makes it ultimately assume some kind of model for the data.
Yes, there can be a lot of flexibility in this model. But one can’t have a truly “model-less model”. Perhaps the AI is based on a huge neural network, with billions of numerical parameters that can get tweaked. Perhaps even the architecture of the network can change. But the whole neural net setup inevitably defines an ultimate underlying model.
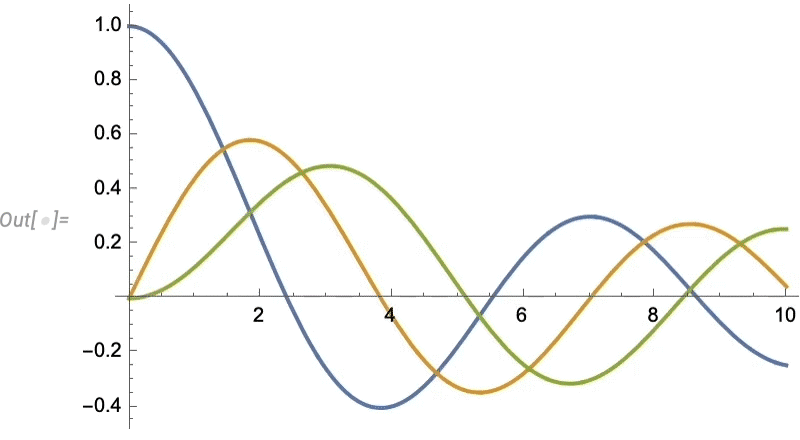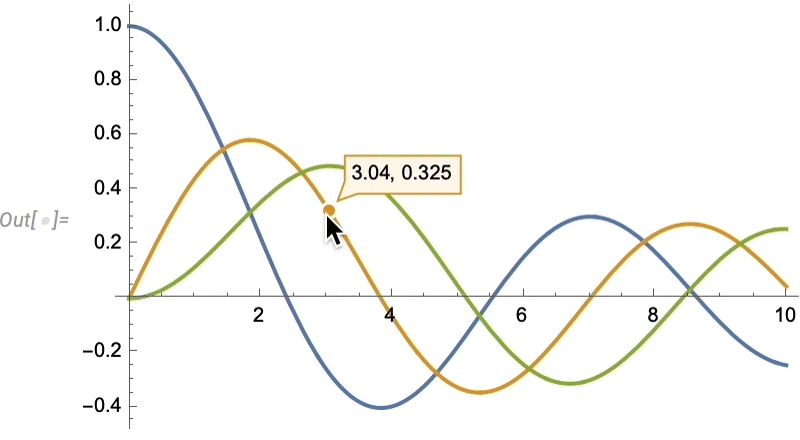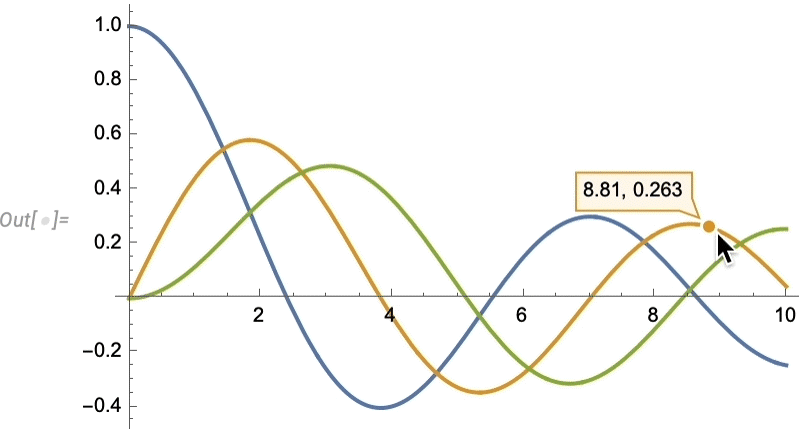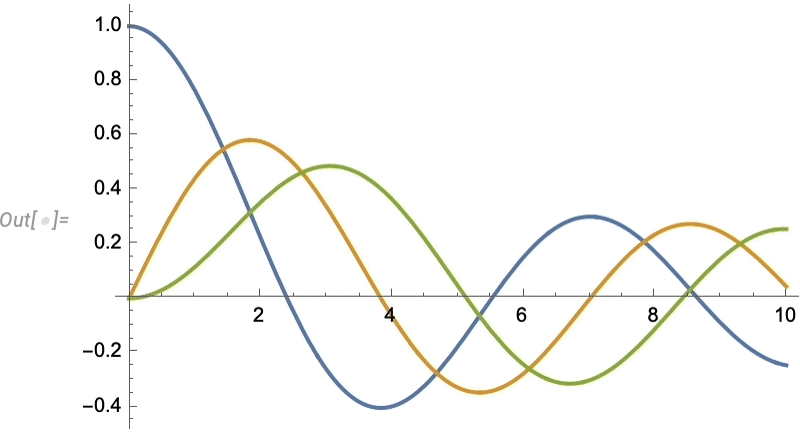
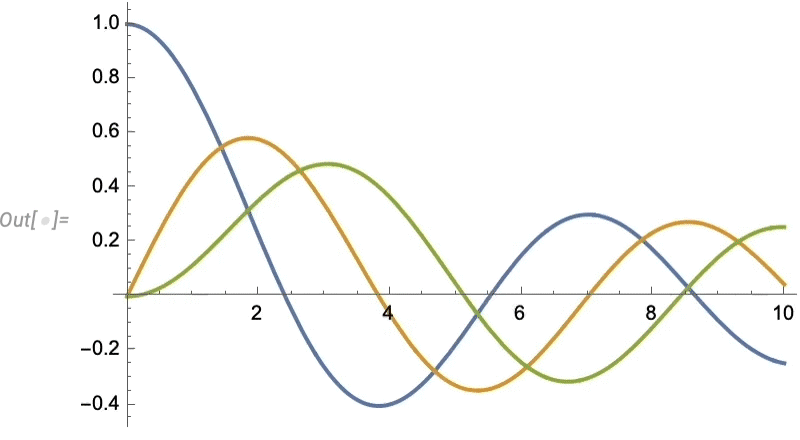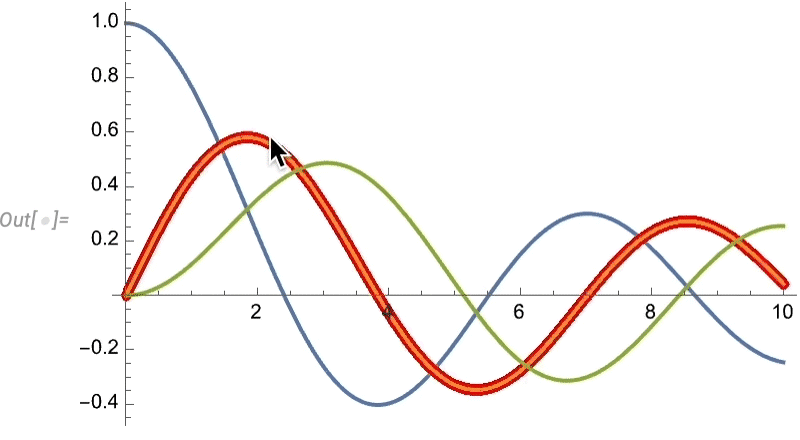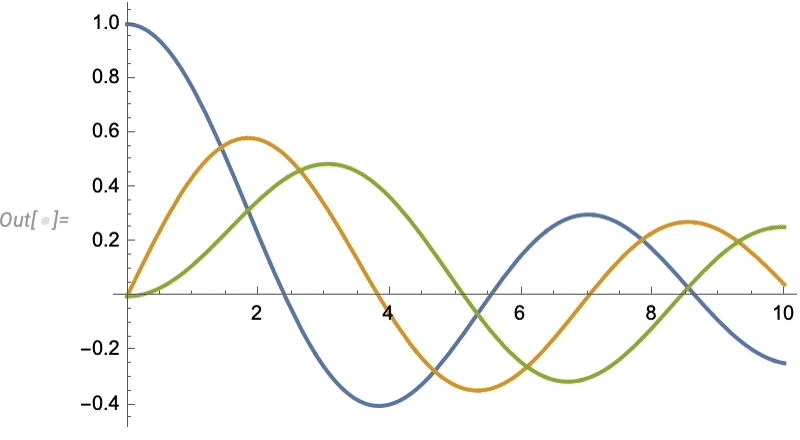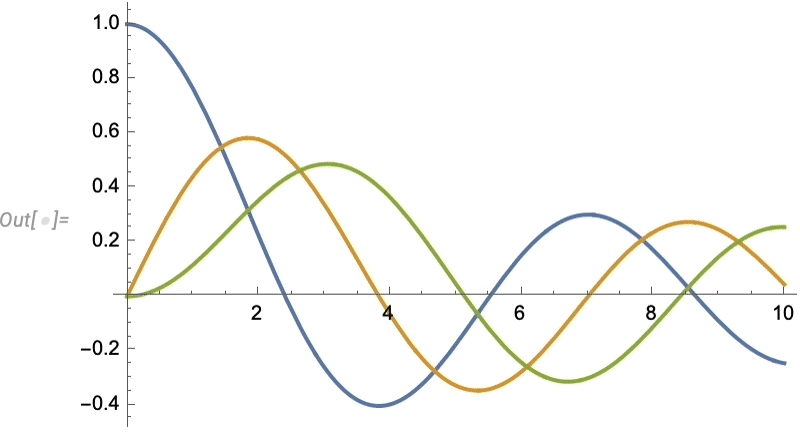
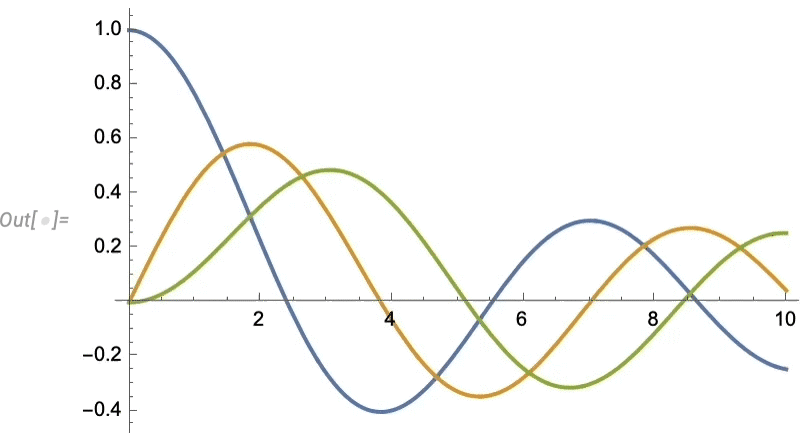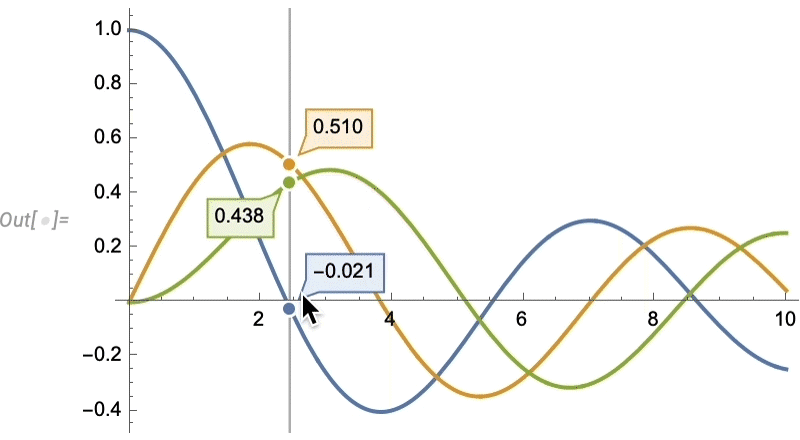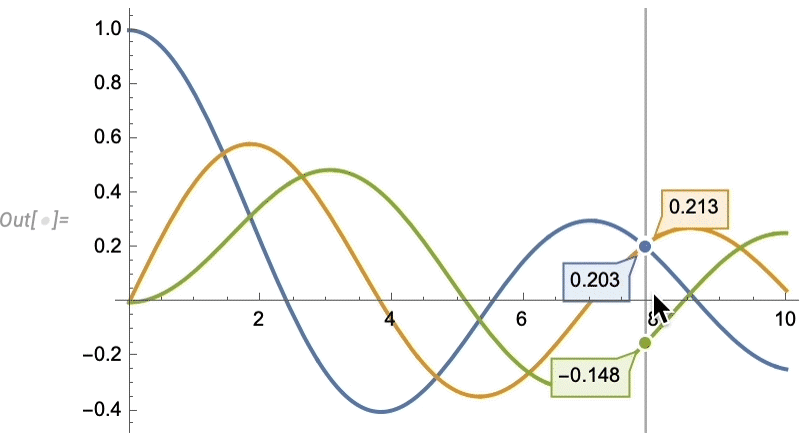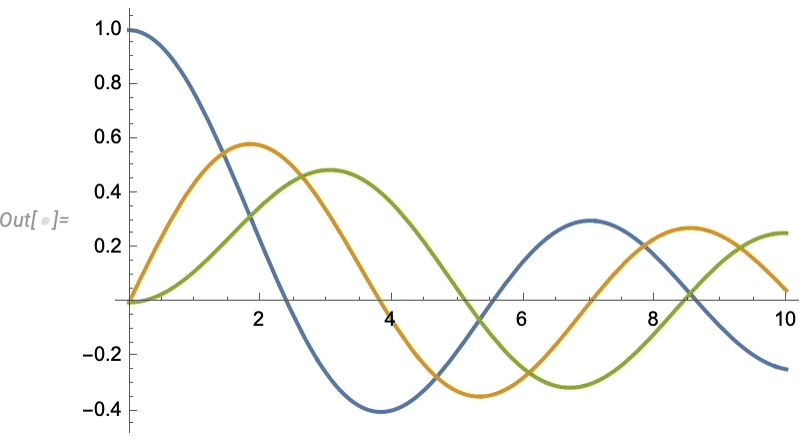
Let’s look at a very simple case. Let’s imagine our “data” is the blue curve here—perhaps representing the motion of a weight suspended on a spring—and that the “physics” tells us it continues with the red curve:
Now let’s take a very simple neural net
and let’s train it using the “blue curve” data above to get a network with a certain collection of weights:
Now let’s apply this trained network to reproduce our original data and extend it:
And what we see is that the network does a decent job of reproducing the data it was trained on, but when it comes to “predicting the future” it basically fails.
So what’s going on here? Did we just not train long enough? Here’s what happens with progressively more rounds of training:
It doesn’t seem like this helps much. So maybe the problem is that our network is too small. Here’s what happens with networks having a series of sizes:
And, yes, larger sizes help. But they don’t solve the problem of making our prediction successful. So what else can we do? Well, one feature of the network is its activation function: how we determine the output at each node from the weighted sum of inputs. Here are some results with various (popular) activation functions:
And there’s something notable here—that highlights the idea that there are “no model-less models”: different activation functions lead to different predictions, and the form of the predictions seems to be a direct reflection of the form of the activation function. And indeed there’s no magic here; it’s just that the neural net corresponds to a function whose core elements are activation functions.
So, for example, the network
corresponds to the function
where ϕ represents the activation function used in this case.
Of course, the idea of approximating one function by some combination of standard functions is extremely old (think: epicycles and before). Neural nets allow one to use more complicated (and hierarchical) combinations of more complicated and nonlinear functions, and provide a more streamlined way of “fitting all the parameters” that are involved. But at a fundamental level it’s the same idea.
And for example here are some approximations to our “data” constructed in terms of more straightforward mathematical functions:
These have the advantage that it’s quite easy to state “what each model is” just by “giving its formula”. But just as with our neural nets, there are problems in making predictions.
(By the way, there are a whole range of methods for things like time series prediction, involving ideas like “fitting to recurrence relations”—and, in modern times, using transformer neural nets. And while some of these methods happen to be able to capture a periodic signal like a sine wave well, one doesn’t expect them to be broadly successful in accurately predicting functions.)
OK, one might say, perhaps we’re trying to use—and train—our neural nets in too narrow a way. After all, it seems as if it was critical to the success of ChatGPT to have a large amount of training data about all kinds of things, not just some narrow specific area. Presumably, though, what that broad training data did was to let ChatGPT learn the “general patterns of language and common sense”, which it just wouldn’t be able to pick up from narrower training data.
So what’s the analog for us here? It might be that we’d want our neural net to have a “general idea of how functions work”—for example to know about things like continuity of functions, or, for that matter, periodicity or symmetry. So, yes, we can go ahead and train not just on a specific “window” of data like we did above, but on whole families of functions—say collections of trigonometric functions, or perhaps all the built-in mathematical functions in the Wolfram Language.
And, needless to say, if we do this, we’ll surely be able to successfully predict our sine curve above—just as we would if we were using traditional Fourier analysis with sine curves as our basis. But is this “doing science”?
In essence it’s saying, “I’ve seen something like this before, so I figure this is what’s going to happen now”. And there’s no question that can be useful; indeed it’s an automated version of a typical thing that a human experienced in some particular area will be able to do. We’ll return to this later. But for now the main point is that at least when it comes to things like predicting functions, it doesn’t seem as if neural nets—and today’s AIs—can in any obvious way “see further” than what goes into their construction and training. There’s no “emergent science”; it’s just fairly direct “pattern matching”.
Predicting Computational Processes
Predicting a function is a particularly austere task and one might imagine that “real processes”—for example in nature—would have more “ambient structure” which an AI could use to get a “foothold” for prediction. And as an example of what we might think of as “artificial nature” we can consider computational systems like cellular automata. Here’s an example of what a particular cellular automaton rule does, with a particular initial condition:
There’s a mixture here of simplicity and complexity. And as humans we can readily predict what’s going to happen in the simple parts, but basically can’t say much about the other parts. So how would an AI do?
Clearly if our “AI” can just run the cellular automaton rule then it will be able to predict everything, though with great computational effort. But the real question is whether an AI can shortcut things to make successful predictions without doing all that computational work—or, put another way, whether the AI can successfully find and exploit pockets of computational reducibility.
So, as a specific experiment, let’s set up a neural net to try to efficiently predict the behavior of our cellular automaton. Our network is basically a straightforward—though “modern”—convolutional autoencoder, with 59 layers and a total of about 800,000 parameters:

It’s trained much like an LLM. We got lots of examples of the evolution of our cellular automaton, then we showed the network the “top half” of each one, and tried to get it to successfully continue this, to predict the “bottom half”. In the specific experiment we did, we gave 32 million examples of 64-cell-wide cellular automaton evolution. (And, yes, this number of examples is tiny compared to all  possible initial configurations.) Then we tried feeding in “chunks” of cellular automaton evolution 64 cells wide and 64 steps long—and looked to see what probabilities the network assigned to different possible continuations.
possible initial configurations.) Then we tried feeding in “chunks” of cellular automaton evolution 64 cells wide and 64 steps long—and looked to see what probabilities the network assigned to different possible continuations.
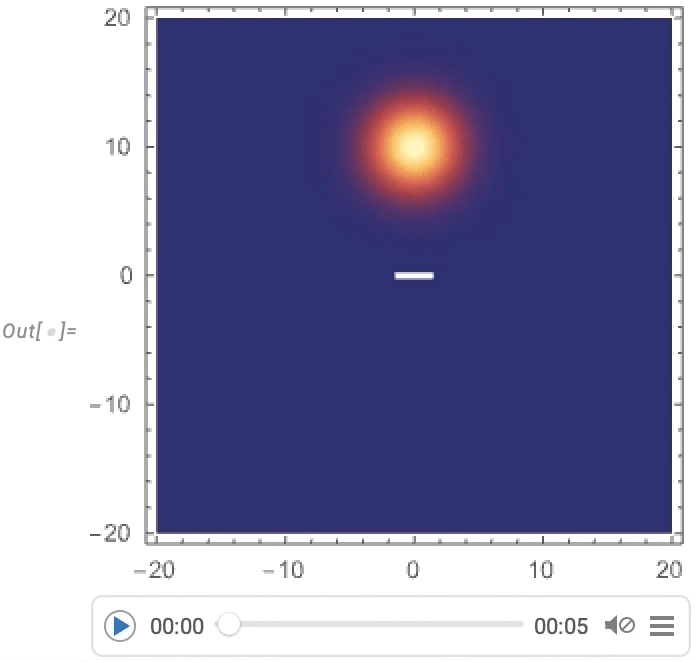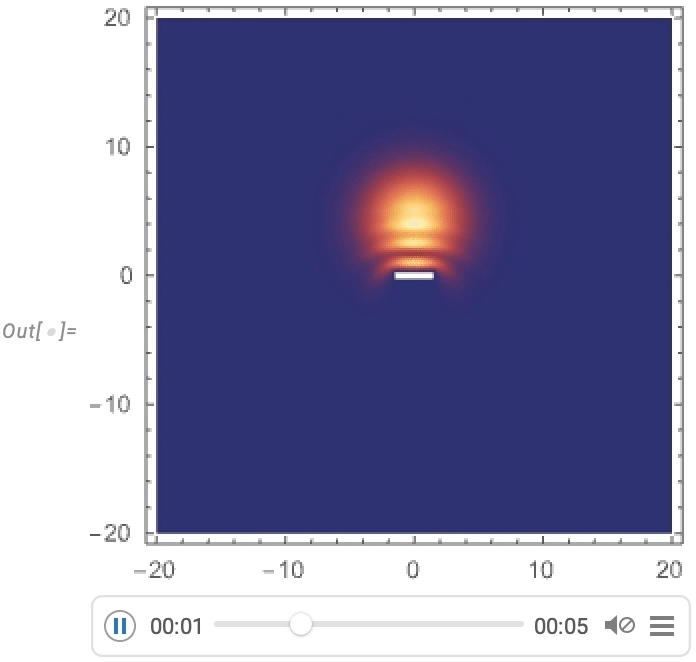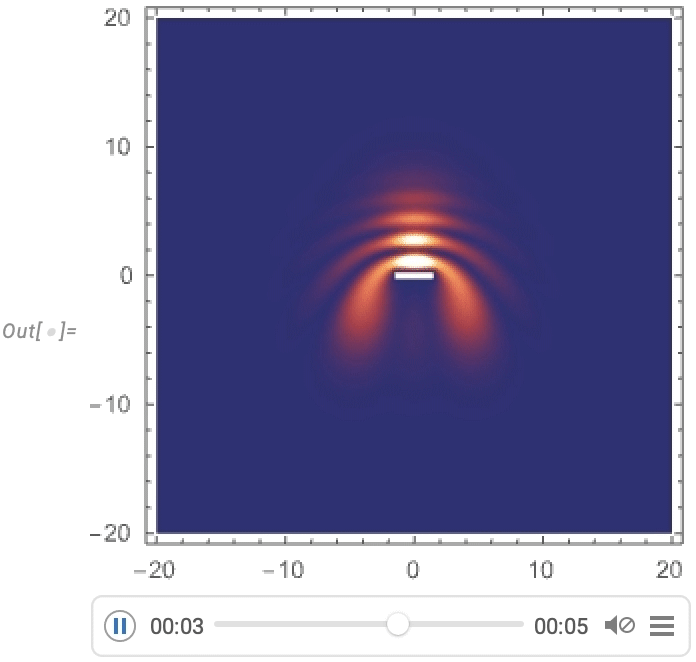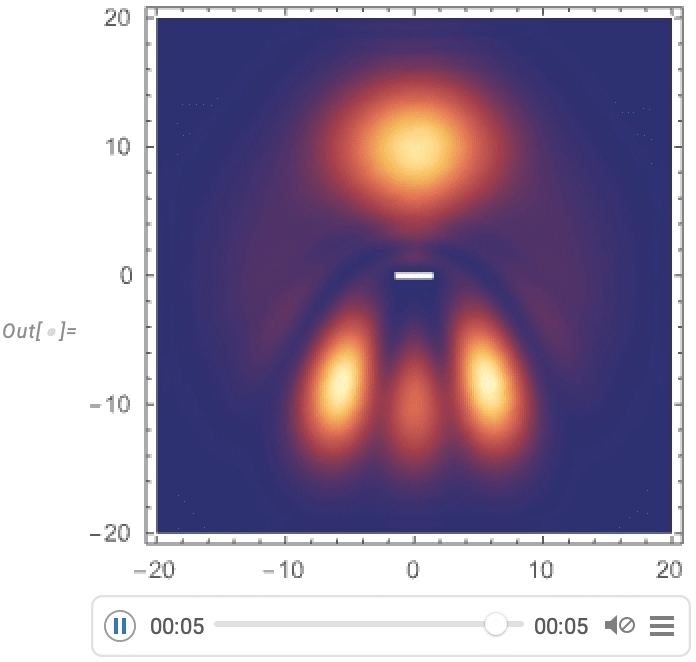
Here are some results for a sequence of different initial conditions:
And what we see is what we might expect: when the behavior is simple enough, the network basically gets it right. But when the behavior is more complicated, the network usually doesn’t do so well with it. It still often gets it at least “vaguely right”—but the details aren’t there.
Perhaps, one might think, the network just wasn’t trained for long enough, or with enough examples. And to get some sense of the effect of more training, here’s how the predicted probabilities evolve with successive quarter million rounds of training:
These should be compared to the exact result:
And, yes, with more training there is improvement, but by the end it seems like it probably won’t get much better. (Though its loss curve does show some sudden downward jumps during the course of training, presumably as “discoveries” are made—and we can’t be sure there won’t be more of these.)
It’s extremely typical of machine learning that it manages to do a good job of getting things “roughly right”. But nailing the details is not what machine learning tends to be good at. So when what one’s trying to do depends on that, machine learning will be limited. And in the prediction task we’re considering here, the issue is that once things go even slightly off track, everything basically just gets worse from there on out.
Identifying Computational Reducibility
Computational reducibility is at the center of what we normally think of as “doing science”. Because it’s not only responsible for letting us make predictions, it’s also what lets us identify regularities, make models and compressed summaries of what we see—and develop understanding that we can capture in our minds.
But how can we find computational reducibility? Sometimes it’s very obvious. Like when we make a visualization of some behavior (like the cellular automaton evolution above) and immediately recognize simple features in it. But in practice computational reducibility may not be so obvious, and we may have to dig through lots of details to find it. And this is a place where AI can potentially help a lot.
At some level we can think of it as a story of “finding the right parametrization” or the “right coordinate system”. As a very straightforward example, consider the seemingly quite random cloud of points:
Just turning this particular cloud of points to the appropriate angle reveals obvious regularities:
But is there a general way to pick out regularities if they’re there? There’s traditional statistics (“Is there a correlation between A and B?”, etc.). There’s model fitting (“Is this a sum of Gaussians?”). There’s traditional data compression (“Is it shorter after run-length encoding?”). But all of these pick out only rather specific kinds of regularities. So can AI do more? Can it perhaps somehow provide a general way to find regularities?
To say one’s found a regularity in something is basically equivalent to saying one doesn’t need to specify all the details of the thing: that there’s a reduced representation from which one can reconstruct it. So, for example, given the “points-lie-on-lines” regularity in the picture above, one doesn’t need to separately specify the positions of all the points; one just needs to know that they form stripes with a certain separation.
OK, so let’s imagine we have an image with a certain number of pixels. We can ask whether there’s reduced representation that involves less data—from which the image can effectively be reconstructed. And with neural nets there’s what one might think of as a trick for finding such a reduced representation.
The basic idea is to set up a neural net as an autoencoder that takes inputs and reproduces them as outputs. One might think this would be a trivial task. But it’s not, because the data from the input has to flow through the innards of the neural net, effectively being “ground up” at the beginning and “reconstituted” at the end. But the point is that with enough examples of possible inputs, it’s potentially possible to train the neural net to successfully reproduce inputs, and operate as an autoencoder.
But now the idea is to look inside the autoencoder, and to pull out a reduced representation that it’s come up with. As data flows from layer to layer in the neural net, it’s always trying to preserve the information it needs to reproduce the original input. And if a layer has fewer elements, what’s present at that layer must correspond to some reduced representation of the original input.
Let’s start with a standard modern image autoencoder, that’s been trained on a few billion images typical of what’s on the web. Feed it a picture of a cat, and it’ll successfully reproduce something that looks like the original picture:
But in the middle there’ll be a reduced representation, with many fewer pixels—that somehow still captures what’s needed of the cat (here shown with its 4 color channels separated):
We can think of this as a kind of “black-box model” for the cat image. We don’t know what the elements (“features”) in the model mean, but somehow it’s successfully capturing “the essence of the picture”.
So what happens if we apply this to “scientific data”, or for example “artificial natural processes” like cellular automata? Here’s a case where we get successful compression:
In this case it’s not quite so successful:
And in these cases—where there’s underlying computational irreducibility—it has trouble:
But there’s a bit more to this story. You see, the autoencoder we’re using was trained on “everyday images”, not these kinds of “scientific images”. So in effect it’s trying to model our scientific images in terms of constructs like eyes and ears that are common in pictures of things like cats.
So what happens if—like in the case of cellular automaton prediction above—we train an autoencoder more specifically on the kinds of images we want?
Here are two very simple neural nets that we can use as an “encoder” and a “decoder” to make an autoencoder:
Now let’s take the standard MNIST image training set, and use these to train the autoencoder:
Each of these images has 28×28 pixels. But in the middle of the autoencoder we have a layer with just two elements. So this means that whatever we ask it to encode must be reduced to just two numbers:
And what we see here is that at least for images that look more or less like the ones it was trained on, the autoencoder manages to reconstruct something that looks at least roughly right, even from the radical compression. If you give it other kinds of images, however, it won’t be as successful, instead basically just insisting on reconstructing them as looking like images from its training set:
OK, so what about training it on cellular automaton images? Let’s take 10 million images generated with a particular rule:
Now we train our autoencoder on these images. Then we try feeding it similar images:
The results are at best very approximate; this small neural net didn’t manage to learn the “detailed ways of this particular cellular automaton”. If it had been successful at characterizing all the apparent complexity of the cellular automaton evolution with just two numbers, then we could have considered this an impressive piece of science. But, unsurprisingly, the neural net was effectively blocked by computational irreducibility.
But even though it can’t “seriously crack computational irreducibility” the neural net can still “make useful discoveries”, in effect by finding little pieces of computational reducibility, and little regularities. So, for example, if we take images of “noisy letters” and use a neural net to reduce them to pairs of numbers, and use these numbers to place the images, we get a “dimension-reduced feature space plot” that separates images of different letters:
But consider, for example, a collection of cellular automata with different rules:
Here’s how a typical neural net would arrange these images in “feature space”:
And, yes, this has almost managed to automatically discover the four classes of behavior that I identified in early 1983. But it’s not quite there. Though in a sense this is a difficult case, very much face-to-face with computational irreducibility. And there are plenty of cases (think: arrangement of the periodic table based on element properties; similarity of fluid flows based on Reynolds number; etc.) where one can expect a neural net to key into pockets of computational reducibility and at least successfully recapitulate existing scientific discoveries.
AI in the Non-human World
In its original concept AI was about developing artificial analogs of human intelligence. And indeed the recent great successes of AI—say in visual object recognition or language generation—are all about having artificial systems that reproduce the essence of what humans do. It’s not that there’s a precise theoretical definition of what makes an image be of a cat versus of a dog. What matters is that we can have a neural net that will come to the same conclusions as humans do.
So why does this work? Probably it’s because neural nets capture the architectural essence of actual brains. Of course the details of artificial neural networks aren’t the same as biological brains. But in a sense the big surprise of modern AI is that there seems to be enough universality to make artificial neural nets behave in ways that are functionally similar to human brains, at least when it comes to things like visual object recognition or language generation.
But what about questions in science? At one level we can ask whether neural nets can emulate what human scientists do. But there’s also another level: is it possible that neural nets can just directly work out how systems—say in nature—behave? Imagine we’re studying some physical process. Human scientists might find some human-level description of the system, say in terms of mathematical equations. But the system itself is just directly doing what it does. And the question is whether that’s something a neural net can capture.
And if neural nets “work” on “human-like tasks” only because they’re architecturally similar to brains, there’s no immediate reason to think that they should be able to capture “raw natural processes” that aren’t anything to do with brains. So what’s going on when AI does something like predicting protein folding?
One part of the story, I suspect, is that even though the physical process of protein folding has nothing to do with humans, the question of what aspects of it we consider significant does. We don’t expect that the neural net will predict the exact position of every atom (and in natural environments the atoms in a protein don’t even have precisely fixed positions). Instead, we want to know things like whether the protein has the “right general shape”, with the right “identifiable features” (like, say, alpha helices), or the right functional properties. And these are now more “human” questions—more in the “eye of the beholder”—and more like a question such as whether we humans judge an image to be of a cat versus a dog. So if we conclude that a neural net “solves the scientific problem” of how a protein folds, it might be at least in part just because the criteria of success that our brains (“subjectively”) apply is something that a neural net—with its brain-like architecture—happens to be able to deliver.
It’s a bit like producing an image with generative AI. At the level of basic human visual perception, it may look like something we recognize. But if we scrutinize it, we can see that it’s not “objectively” what we think it is:
It wasn’t ever really practical with “first-principles physics” to figure out how proteins fold. So the fact that neural nets can get even roughly correct answers is impressive. So how do they do it? A significant part of it is surely effectively just matching chunks of protein to what’s in the training set—and then finding “plausible” ways to “stitch” these chunks together. But there’s probably something else too. One’s familiar with certain “pieces of regularity” in proteins (things like alpha helices and beta sheets). But it seems likely that neural nets are effectively plugging into other kinds of regularity; they’ve somehow found pockets of reducibility that we didn’t know were there. And particularly if just a few pockets of reducibility show up over and over again, they’ll effectively represent new, general “results in science” (say, some new kind of commonly occurring “meta-motif” in protein structure).
But while it’s fundamentally inevitable that there must be an infinite number of pockets of computational reducibility in the end, it’s not clear at the outset either how significant these might be in things we care about, or how successful neural net methods might be in finding them. We might imagine that insofar as neural nets mirror the essential operation of our brains, they’d only be able to find pockets of reducibility in cases where we humans could also readily discover them, say by looking at some visualization or another.
But an important point is that our brains are normally “trained” only on data that we readily experience with our senses: we’ve seen the equivalent of billions of images, and we’ve heard zillions of sounds. But we don’t have direct experience of the microscopic motions of molecules, or of a multitude of kinds of data that scientific observations and measuring devices can deliver.
A neural net, however, can “grow up” with very different “sensory experiences”—say directly experiencing “chemical space”, or, for that matter “metamathematical space”, or the space of financial transactions, or interactions between biological organisms, or whatever. But what kinds of pockets of computational reducibility exist in such cases? Mostly we don’t know. We know the ones that correspond to “known science”. But even though we can expect others must exist, we don’t normally know what they are.
Will they be “accessible” to neural nets? Again, we don’t know. Quite likely, if they are accessible, then there’ll be some representation—or, say, visualization—in which the reducibility will be “obvious” to us. But there are plenty of ways this could fail. For example, the reducibility could be “visually obvious”, but only, say, in 3D volumes where, for example, it’s hard even to distinguish different structures of fluffy clouds. Or perhaps the reducibility could be revealed only through some computation that’s not readily handled by a neural net.
Inevitably there are many systems that show computational irreducibility, and which—at least in their full form—must be inaccessible to any “shortcut method”, based on neural nets or otherwise. But what we’re asking is whether, when there is a pocket of computational reducibility, it can be captured by a neural net.
But once again we’re confronted with the fact there are no “model-less models”. Some particular kind of neural net will readily be able to capture some particular kinds of computational reducibility; another will readily be able to capture others. And, yes, you can always construct a neural net that will approximate any given specific function. But in capturing some general kind of computational reducibility, we are asking for much more—and what we can get will inevitably depend on the underlying structure of the neural net.
But let’s say we’ve got a neural net to successfully key into computational reducibility in a particular system. Does that mean it can predict everything? Typically no. Because almost always the computational reducibility is “just a pocket”, and there’s plenty of computational irreducibility—and “surprises”—“outside”.
And indeed this seems to happen even in the case of something like protein folding. Here are some examples of proteins with what we perceive as fairly simple structures—and the neural net prediction (in yellow) agrees quite well with the results of physical experiments (gray tubes):
But for proteins with what we perceive as more complicated structures, the agreement is often not nearly as good:
These proteins are all are at least similar to ones that were used to train the neural net. But how about very different proteins—say ones with random sequences of amino acids?
It’s hard to know how well the neural net does here; it seems likely that particularly if there are “surprises” it won’t successfully capture them. (Of course, it could be that all “reasonable proteins” that normally appear in biology could have certain features, and it could be “unfair” to apply the neural net to “unbiological” random ones—though for example in the adaptive immune system, biology does effectively generate at least short “random proteins”.)
Solving Equations with AI
In traditional mathematical science the typical setup is: here are some equations for a system; solve them to find out how the system behaves. And before computers, that usually meant that one had to find some “closed-form” formula for the solution. But with computers, there’s an alternative approach: make a discrete “numerical approximation”, and somehow incrementally solve the equations. To get accurate results, though, may require many steps and lots of computational effort. So then the question is: can AI speed this up? And in particular, can AI, for example, go directly from initial conditions for an equation to a whole solution?
Let’s consider as an example a classical piece of mathematical physics: the three-body problem. Given initial positions and velocities of three point masses interacting via inverse-square-law gravity, what trajectories will the masses follow? There’s a lot of diversity—and often a lot of complexity—which is why the three-body problem has been such a challenge:
But what if we train a neural net on lots of sample solutions? Can it then figure out the solution in any particular case? We’ll use a rather straightforward “multilayer perceptron” network:
We feed it initial conditions, then ask it to generate a solution. Here are a few examples of what it does, with the correct solutions indicated by the lighter background paths:
When the trajectories are fairly simple, the neural net does decently well. But when things get more complicated, it does decreasingly well. It’s as if the neural net has “successfully memorized” the simple cases, but doesn’t know what to do in more complicated cases. And in the end this is very similar to what we saw above in examples like predicting cellular automaton evolution (and presumably also protein folding).
And, yes, once again this is a story of computational irreducibility. To ask to just “get the solution” in one go is to effectively ask for complete computational reducibility. And insofar as one might imagine that—if only one knew how to do it—one could in principle always get a “closed-form formula” for the solution, one’s implicitly assuming computational reducibility. But for many decades I’ve thought that something like the three-body problem is actually quite full of computational irreducibility.
Of course, had a neural net been able to “crack the problem” and immediately generate solutions, that would effectively have demonstrated computational reducibility. But as it is, the apparent failure of neural nets provides another piece of evidence for computational irreducibility in the three-body problem. (It’s worth mentioning, by the way, that while the three-body problem does show sensitive dependence on initial conditions, that’s not the primary issue here; rather, it’s the actual intrinsic complexity of the trajectories.)
We already know that discrete computational systems like cellular automata are rife with computational irreducibility. And we might have imagined that continuous systems—described for example by differential equations—would have more structure that would somehow make them avoid computational irreducibility. And indeed insofar as neural nets (in their usual formulation) involve continuous numbers, we might have thought that they would be able in some way to key into the structure of continuous systems to be able to predict them. But somehow it seems as if the “force of computational irreducibility” is too strong, and will ultimately be beyond the power of neural networks.
Having said that, though, there can still be a lot of practical value to neural networks in doing things like solving equations. Traditional numerical approximation methods tend to work locally and incrementally (if often adaptively). But neural nets can more readily handle “much larger windows”, in a sense “knowing longer runs of behavior” and being able to “jump ahead” across them. In addition, when one’s dealing with very large numbers of equations (say in robotics or systems engineering), neural nets can typically just “take in all the equations and do something reasonable” whereas traditional methods effectively have to work with the equations one by one.
The three-body problem involves ordinary differential equations. But many practical problems are instead based on partial differential equations (PDEs), in which not just individual coordinates, but whole functions f[x] etc., evolve with time. And, yes, one can use neural nets here as well, often to significant practical advantage. But what about computational irreducibility? Many of the equations and situations most studied in practice (say for engineering purposes) tend to avoid it, but certainly in general it’s there (notably, say, in phenomena like fluid turbulence). And when there’s computational irreducibility, one can’t ultimately expect neural nets to do well. But when it comes to satisfying our human purposes—as in other examples we’ve discussed—things may look better.
As an example, consider predicting the weather. In the end, this is all about PDEs for fluid dynamics (and, yes, there are also other effects to do with clouds, etc.). And as one approach, one can imagine directly and computationally solving these PDEs. But another approach would be to have a neural net just “learn typical patterns of weather” (as old-time meteorologists had to), and then have the network (a bit like for protein folding) try to patch together these patterns to fit whatever situation arises.
How successful will this be? It’ll probably depend on what we’re looking at. It could be that some particular aspect of the weather shows considerable computational reducibility and is quite predictable, say by neural nets. And if this is the aspect of the weather that we care about, we might conclude that the neural net is doing well. But if something we care about (“will it rain tomorrow?”) doesn’t tap into a pocket of computational reducibility, then neural nets typically won’t be successful in predicting it—and instead there’d be no choice but to do explicit computation, and perhaps impractically much of it.
AI for Multicomputation
In what we’ve discussed so far, we’ve mostly been concerned with seeing whether AI can help us “jump ahead” and shortcut some computational process or another. But there are also lots of situations where what’s of interest is instead to shortcut what one can call a multicomputational process, in which there are many possible outcomes at each step, and the goal is for example to find a path to some final outcome.
As a simple example of a multicomputational process, let’s consider a multiway system operating on strings, where at each step we apply the rules {A  BBB, BB
BBB, BB  A} in all possible ways:
A} in all possible ways:
Given this setup we can ask a question like: what’s the shortest path from A to BABA? And in the case shown here it’s easy to compute the answer, say by explicitly running a pathfinding algorithm on the graph:
There are many kinds of problems that follow this same general pattern. Finding a winning sequence of plays in a game graph. Finding the solution to a puzzle as a sequence of moves through a graph of possibilities. Finding a proof of a theorem given certain axioms. Finding a chemical synthesis pathway given certain basic reactions. And in general solving a multitude of NP problems in which many “nondeterministic” paths of computation are possible.
In the very simple example above, we’re readily able to explicitly generate a whole multiway graph. But in most practical examples, the graph would be astronomically too large. So the challenge is typically to suss out what moves to make without tracing the whole graph of possibilities. One common approach is to try to find a way to assign a score to different possible states or outcomes, and to pursue only paths with (say) the highest scores. In automated theorem proving it’s also common to work “downward from initial propositions” and “upward from final theorems”, trying to see where the paths meet in the middle. And there’s also another important idea: if one has established the “lemma” that there’s a path from X to Y, one can add X  Y as a new rule in the collection of rules.
Y as a new rule in the collection of rules.
So how might AI help? As a first approach, we could consider taking something like our string multiway system above, and training what amounts to a language-model AI to generate sequences of tokens that represent paths (or what in a mathematical setting would be proofs). The idea is to feed the AI a collection of valid sequences, and then to present it with the beginning and end of a new sequence, and ask it to fill in the middle.
We’ll use a fairly basic transformer network:
Then we train it by giving lots of sequences of tokens corresponding to valid paths (with E being the “end token”)
together with “negative examples” indicating the absence of paths:
Now we “prompt” the trained network with a “prefix” of the kind that appeared in the training data, and then iteratively run “LLM style” (effectively at zero temperature, i.e. always choosing the “most probable” next token):
For a while, it does perfectly—but near the end it starts making errors, as indicated by the tokens shown in red. There’s different performance with different destinations—with some cases going off track right at the beginning:
How can we do better? One possibility is at each step to keep not just the token that’s considered most probable, but a stack of tokens—thereby in effect generating a multiway system that the “LLM controller” could potentially navigate. (One can think of this somewhat whimsically as a “quantum LLM”, that’s always exploring multiple paths of history.)
(By the way, we could also imagine training with many different rules, then doing what amounts to zero-shot learning and giving a “pre-prompt” that specifies what rule we want to use in any particular case.)
One of the issues with this LLM approach is that the sequences it generates are often even “locally wrong”: the next element can’t follow from the one before according to the rules given.
But this suggests another approach one can take. Instead of having the AI try to “immediately fill in the whole sequence”, get it instead just to pick “where to go next”, always following one of the specified rules. Then a simple goal for training is in effect to get the AI to learn the distance function for the graph, or in other words, to be able to estimate how long the shortest path is (if it exists) from any one node to any other. Given such a function, a typical strategy is to follow what amounts to a path of “steepest descent”—at each step picking the move that the AI estimates will do best in reducing the distance to the destination.
How can this actually be implemented with neural networks? One approach is to use two encoders (say constructed out of transformers)—that in effect generate two embeddings, one for source nodes, and one for destination nodes. The network then combines these embeddings and learns a “metric” that characterizes the distance between the nodes:
Training such a network on the multiway system we’ve been discussing—by giving it a few million examples of source-destination distances (plus an indicator of whether this distance is infinite)—we can use the network to predict a piece of the distance matrix for the multiway system. And what we find is that this predicted matrix is similar—but definitely not identical—to the actual matrix:
Still, we can imagine trying to build a path where at each step we compute the estimated distances-to-destination predicted by the neural net for each possible destination, then pick the one that “gets furthest”:
Each individual move here is guaranteed to be valid, and we do indeed eventually reach our destination BABA—though in slightly more steps than the true shortest path. But even though we don’t quite find the optimal path, the neural net has managed to allow us to at least somewhat prune our “search space”, by prioritizing nodes and traversing only the red edges:
(A technical point is that the particular neural net we’ve used here has the property that all paths between any given pair of nodes always have the same length—so if any path is found, it can be considered “the shortest”. A rule like {A  AAB, BBA
AAB, BBA  B} doesn’t have this property and a neural net trained for this rule can end up finding paths that reach the correct destination but aren’t as short as they could be.)
B} doesn’t have this property and a neural net trained for this rule can end up finding paths that reach the correct destination but aren’t as short as they could be.)
Still, as is typical with neural nets, we can’t be sure how well this will work. The neural net might make us go arbitrarily far “off track”, and it might even lead us to a node where we have no path to our destination—so that if we want to make progress we’ll have to resort to something like traditional algorithmic backtracking.
But at least in simple cases the approach can potentially work well—and the AI can successfully find a path that wins the game, proves the theorem, etc. But one can’t expect it to always work. And the reason is that it’s going to run into multicomputational irreducibility. Just as in a single “thread of computation” computational irreducibility can mean that there’s no shortcut to just “going through the steps of the computation”, so in a multiway system multicomputational irreducibility can mean that there’s no shortcut to just “following all the threads of computation”, then seeing, for example, which end up merging with which.
But even though this could happen in principle, does it in fact happen in practice in cases of interest to us humans? In something like games or puzzles, we tend to want it to be hard—but not too hard—to “win”. And when it comes to mathematics and proving theorems, cases that we use for exercises or competitions we similarly want to be hard, but not too hard. But when it comes to mathematical research, and the frontiers of mathematics, one doesn’t immediately expect any such constraint. And the result is then that one can expect to be face-to-face with multicomputational irreducibility—making it hard for AI to help too much.
There is, however, one footnote to this story, and it has to do with how we choose new directions in mathematics. We can think of a metamathematical space formed by building up theorems from other theorems in all possible ways in a giant multiway graph. But as we’ll discuss below, most of the details of this are far from what human mathematicians would think of as “doing mathematics”. Instead, mathematicians implicitly seem to do mathematics at a “higher level” in which they’ve “coarse grained” this “microscopic metamathematics”—much as we might study a physical fluid in terms of comparatively-simple-to-describe continuous dynamics even though “underneath” there are lots of complicated molecular motions.
So can AI help with mathematics at this “fluid-dynamics-style” level? Potentially so, but mainly in what amounts to providing code assistance. We have something we want to express, say, in Wolfram Language. But we need help—“LLM style”—in going from our informal conception to explicit computational language. And insofar as what we’re doing follows the structural patterns of what’s been done before, we can expect something like an LLM to help. But insofar as what we’re expressing is “truly new”, and inasmuch as our computational language doesn’t involve much “boilerplate”, it’s hard to imagine that an AI trained on what’s been done before will help much. Instead, what we in effect have to do is some multicomputationally irreducible computation, that allows us to explore to some fresh part of the computational universe and the ruliad.
Exploring Spaces of Systems
“Can one find a system that does X?” Say a Turing machine that runs for a very long time before halting. Or a cellular automaton that grows, but only very slowly. Or, for that matter, a chemical with some particular property.
This is a somewhat different type of question than the ones we’ve been discussing so far. It’s not about taking a particular rule and seeing what its consequences are. It’s about identifying what rule might exist that has certain consequences.
And given some space of possible rules, one approach is exhaustive search. And in a sense this is ultimately the only “truly unbiased” approach, that will discover what’s out there to discover, even when one doesn’t expect it. Of course, even with exhaustive search, one still needs a way to determine whether a particular candidate system meets whatever criterion one has set up. But now this is the problem of predicting a computation—where the things we said above apply.
OK, but can we do better than exhaustive search? And can we, for example, find a way to figure out what rules to explore without having to look at every rule? One approach is to do something like what happens in biological evolution by natural selection: start, say, from a particular rule, and then incrementally change it (perhaps at random), at every step keeping the rule or rules that do best, and discarding the others.
This isn’t “AI” as we’ve operationally defined it here (it’s more like a “genetic algorithm”)—though it is a bit like the inner training loop of a neural net. But will it work? Well, that depends on the structure of the rule space—and, as one sees in machine learning—it tends to work better in higher-dimensional rule spaces than lower-dimensional ones. Because with more dimensions there’s less chance one will get “stuck in a local minimum”, unable to find one’s way out to a “better rule”.
And in general, if the rule space is like a complicated fractal mountainscape, it’s reasonable to expect one can make progress incrementally (and perhaps AI methods like reinforcement learning can help refine what incremental steps to take). But if instead it’s quite flat, with, say, just one “hole” somewhere (“golf-course style”), one can’t expect to “find the hole” incrementally. So what is the typical structure of rule spaces? There are certainly plenty of cases where the rule space is altogether quite large, but the number of dimensions is only modest. And in such cases (an example being finding small Turing machines with long halting times) there often seem to be “isolated solutions” that can’t be reached incrementally. But when there are more dimensions, it seems likely that what amounts to computational irreducibility will more or less guarantee that there’ll be a “random-enough landscape” that incremental methods will be able to do well, much as we have seen in machine learning in recent years.
So what about AI? Might there be a way for AI to learn how to “pick winners directly in rule space”, without any kind of incremental process? Might we perhaps be able to find some “embedding space” in which the rules we want are laid out in a simple way—and thus effectively “pre-identified” for us? Ultimately it depends on what the rule space is like, and whether the process of exploring it is necessarily (multi)computationally irreducible, or whether at least the aspects of it that we care about can be explored by a computationally reducible process. (By the way, trying to use AI to directly find systems with particular properties is a bit like trying to use AI to directly generate neural nets from data without incremental training.)
Let’s look at a specific simple example based on cellular automata. Say we want to find a cellular automaton rule that—when evolved from a single-cell initial condition—will grow for a while, but then die out after a particular, exact number of steps. We can try to solve this with a very minimal AI-like “evolutionary” approach: start from a random rule, then at each “generation” produce a certain number of “offspring” rules, each with one element randomly changed—then keep whichever is the “best” of these rules. If we want to find a rule that “lives” for exactly 50 steps, we define “best” to be the one that minimizes a “loss function” equal to the distance from 50 of the number of steps a rule actually “lives”.
So, for example, say we start from the randomly chosen (3-color) rule:
Our evolutionary sequence of rules (showing here only the  “outcome values”) might be:
“outcome values”) might be:
If we look at the behavior of these rules, we see that—after an inauspicious start—they manage to successfully evolve to reach a rule that meets the criterion of “living for exactly 50 steps”:
What we’ve shown here is a particular randomly chosen “path of evolution”. But what happens with other paths? Here’s how the “loss” evolves (over the course of 100 generations) for a collection of paths:
And what we see is that there’s only one “winner” here that achieves zero loss; on all the other paths, evolution “gets stuck”.
As we mentioned above, though, with more “dimensions” one’s less likely to get stuck. So, for example, if we look at 4-color cellular automaton rules, there are now 64 rather than 27 possible elements (or effectively dimensions) to change, and in this case, many paths of evolution “get further”
and there are more “winners” such as:
How could something like neural nets help us here? Insofar as we can use them to predict cellular automaton evolution, they might give us a way to speed up what amounts to the computation of the loss for each candidate rule—though from what we saw in an earlier section, computational irreducibility is likely to limit this. Another possibility is that—much as in the previous section—we could try to use neural nets to guide us in which random changes to make at each generation. But while computational irreducibility probably helps in making things “effectively random enough” that we won’t get stuck, it makes it difficult to have something like a neural net successfully tell us “which way to go”.
Science as Narrative
In many ways one can view the essence of science—at least as it’s traditionally been practiced—as being about taking what’s out there in the world and somehow casting it in a form we humans can think about. In effect, we want science to provide a human-accessible narrative for what happens, say in the natural world.
The phenomenon of computational irreducibility now shows us that this will often ultimately not be possible. But whenever there’s a pocket of computational reducibility it means that there’s some kind of reduced description of at least some part of what’s going on. But is that reduced description something that a human could reasonably be expected to understand? Can it, for example, be stated succinctly in words, formulas, or computational language? If it can, then we can think of it as representing a successful “human-level scientific explanation”.
So can AI help us automatically create such explanations? To do so it must in a sense have a model for what we humans understand—and how we express this understanding in words, etc. It doesn’t do much good to say “here are 100 computational steps that produce this result”. To get a “human-level explanation” we need to break this down into pieces that humans can assimilate.
As an example, consider a mathematical proof, generated by automated theorem proving:

A computer can readily check that this is correct, in that each step follows from what comes before. But what we have here is a very “non-human thing”—about which there’s no realistic “human narrative”. So what would it take to make such a narrative? Essentially we’d need “waypoints” that are somehow familiar—perhaps famous theorems that we readily recognize. Of course there may be no such things. Because what we may have is a proof that goes through “uncharted metamathematical territory”. So—AI assisted or not—human mathematics as it exists today may just not have the raw material to let us create a human-level narrative.
In practice, when there’s a fairly “short metamathematical distance” between steps in a proof, it’s realistic to think that a human-level explanation can be given. And what’s needed is very much like what Wolfram|Alpha does when it produces step-by-step explanations of its answers. Can AI help? Potentially, using methods like our second approach to AI-assisted multicomputation above.
And, by the way, our efforts with Wolfram Language help too. Because the whole idea of our computational language is to capture “common lumps of computational work” as built-in constructs—and in a sense the process of designing the language is precisely about identifying “human-assimilable waypoints” for computations. Computational irreducibility tells us that we’ll never be able to find such waypoints for all computations. But our goal is to find waypoints that capture current paradigms and current practice, as well as to define directions and frameworks for extending these—though ultimately “what we humans know about” is something that’s determined by the state of human knowledge as it’s historically evolved.
Proofs and computational language programs are two examples of structured “scientific narratives”. A potentially simpler example—aligned with the mathematical tradition for science—is a pure formula. “It’s a power law”. “It’s a sum of exponentials”. Etc. Can AI help with this? A function like FindFormula is already using machine-learning-inspired techniques to take data and try to produce a “reasonable formula for it”.
Here’s what it does for the first 100 primes:
Going to 10,000 primes it produces a more complicated result:
Or, let’s say we ask about the relation between GDP and population for countries. Then we can get formulas like:
But what (if anything) do these formulas mean? It’s a bit like with proof steps and so on. Unless we can connect what’s in the formulas with things we know about (whether in number theory or economics) it’ll usually be difficult to conclude much from them. Except perhaps in some rare cases where one can say “yes, that’s a new, useful law”—like in this “derivation” of Kepler’s third law (where 0.7 is a pretty good approximation to 2/3):
There’s an even more minimal example of this kind of thing in recognizing numbers. Type a number into Wolfram|Alpha and it’ll try to tell you what “possible closed forms” for the number might be:

There are all sorts of tradeoffs here, some very AI informed. What’s the relative importance of getting more digits right compared to having a simple formula? What about having simple numbers in the formula compared to having “more obscure” mathematical constants (e.g. π versus Champernowne’s number)? When we set up this system for Wolfram|Alpha 15 years ago, we used the negative log frequency of constants in the mathematical literature as a proxy for their “information content”. With modern LLM techniques it may be possible to do a more holistic job of finding what amounts to a “good scientific narrative” for a number.
But let’s return to things like predicting the outcome of processes such as cellular automaton evolution. In an earlier section we discussed getting neural nets to do this prediction. We viewed this essentially as a “black-box” approach: we wanted to see if we could get a neural net to successfully make predictions, but we weren’t asking to get a “human-level understanding” of those predictions.
It’s a ubiquitous story in machine learning. One trains a neural net to successfully predict, classify, or whatever. But if one “looks inside” it’s very hard to tell what’s going on. Here’s the final result of applying an image identification neural network:
And here are the “intermediate thoughts” generated after going through about half the layers in the network:
Maybe something here is a “definitive signature of catness”. But it’s not part of our current scientific lexicon—so we can’t usefully use it to develop a “scientific narrative” that explains how the image should be interpreted.
But what if we could reduce our images to just a few parameters—say using an autoencoder of the kind we discussed above? Conceivably we could set things up so that we’d end up with “interpretable parameters”—or, in other words, parameters where we can give a narrative explanation of what they mean. For example, we could imagine using something like an LLM to pick parameters that somehow align with words or phrases (“pointiness”, “fractal dimension”, etc.) that appear in explanatory text from around the web. And, yes, these words or phrases could be based on analogies (“cactus-shaped”, “cirrus-cloud-like”, etc.)—and something like an LLM could “creatively” come up with these names.
But in the end there’s nothing to say that a pocket of computational reducibility picked out by a certain autoencoder will have any way to be aligned with concepts (scientific or otherwise) that we humans have yet explored, or so far given words to. Indeed, in the ruliad at large, it is overwhelmingly likely that we’ll find ourselves in “interconcept space”—unable to create what we would consider a useful scientific narrative.
This depends a bit, however, on just how we constrain what we’re looking at. We might implicitly define science to be the study of phenomena for which we have—at some time—successfully developed a scientific narrative. And in this case it’s of course inevitable that such a narrative will exist. But even given a fixed method of observation or measurement it’s basically inevitable that as we explore, computational irreducibility will lead to “surprises” that break out of whatever scientific narrative we were using. Or in other words, if we’re really going to discover new science, then—AI or not—we can’t expect to have a scientific narrative based on preexisting concepts. And perhaps the best we can hope for is that we’ll be able to find pockets of reducibility, and that AI will “understand” enough about us and our intellectual history that it’ll be able to suggest a manageable path of new concepts that we should learn to develop a successful scientific narrative for what we discover.
Finding What’s Interesting
A central part of doing open-ended science is figuring out “what’s interesting”. Let’s say one just enumerates a collection of cellular automata:
The ones that just die out—or make uniform patterns—“don’t seem interesting”. The first time one sees a nested pattern generated by a cellular automaton, it might seem interesting (as it did to me in 1981). But pretty soon it comes to seem routine. And at least as a matter of basic ruliology, what one ends up looking for is “surprise”: qualitatively new behavior one hasn’t seen before. (If one’s concerned with specific applications, say to modeling particular systems in the world, then one might instead want to look at rules with certain structure, whether or not their behavior “abstractly seems interesting”.)
The fact that one can expect “surprises” (and indeed, be able to do useful, truly open-ended science at all) is a consequence of computational irreducibility. And whenever there’s a “lack of surprise” it’s basically a sign of computational reducibility. And this makes it plausible that AI—and neural nets—could learn to identify at least certain kinds of “anomalies” or “surprises”, and thereby discover some version of “what’s interesting”.
Usually the basic idea is to have a neural net learn the “typical distribution” of data—and then to identify outliers relative to this. So for example we might look at a large number of cellular automaton patterns to learn their “typical distribution”, then plot a projection of this onto a 2D feature space, indicating where certain specific patterns lie:
Some of the patterns show up in parts of the distribution where their probabilities are high, but others show up where the probabilities are low—and these are the outliers:
Are these outliers “interesting”? Well, it depends on your definition of “interesting”. And in the end that’s “in the eye of the beholder”. Here, the “beholder” is a neural net. And, yes, these particular patterns wouldn’t be what I would have picked. But relative to the “typical patterns” they do seem at least “somewhat different”. And presumably it’s basically a story like the one with neural nets that distinguish pictures of cats and dogs: neural nets make at least somewhat similar judgements to the ones we do—perhaps because our brains are structurally like neural nets.
OK, but what does a neural net “intrinsically find interesting”? If the neural net is trained then it’ll very much be influenced by what we can think of as the “cultural background” it gets from this training. But what if we just set up neural nets with a given architecture, and pick their weights at random? Let’s say they’re neural nets that compute functions  . Then here are examples of collections of functions they compute:
. Then here are examples of collections of functions they compute:
Not too surprisingly, the functions that come out very much reflect the underlying activation functions that appear at the nodes of our neural nets. But we can see that—a bit like in a random walk process—“more extreme” functions are less likely to be produced by neural nets with random weights, so can be thought of as “intrinsically more surprising” for neural nets.
But, OK, “surprise” is one potential criterion for “interestingness”. But there are others. And to get a sense of this we can look at various kinds of constructs that can be enumerated, and where we can ask which possible ones we consider “interesting enough” that we’ve, for example, studied them, given them specific names, or recorded them in registries.
As a first example, let’s consider a family of hydrocarbon molecules: alkanes. Any such molecule can be represented by a tree graph with nodes corresponding to carbon atoms, and having valence at most 4. There are a total of 75 alkanes with 10 or fewer carbons, and all of them typically appear in standard lists of chemicals (and in our Wolfram Knowledgebase). But with 10 carbons only some alkanes are “interesting enough” that they’re listed, for example in our knowledgebase (aggregating different registries one finds more alkanes listed, but by 11 carbons at least 42 out of 159 always seem to be “missing”—and are not highlighted here):
What makes some of these alkanes be considered “more interesting” in this sense than others? Operationally it’s a question of whether they’ve been studied, say in the academic literature. But what determines this? Partly it’s a matter of whether they “occur in nature”. Sometimes—say in petroleum or coal—alkanes form through what amount to “random reactions”, where unbranched molecules tend to be favored. But alkanes can also be produced in biological systems, through careful orchestration, say by enzymes. But wherever they come from, it’s as if the alkanes that are more familiar are the ones that seem “more interesting”. So what about “surprise”? Whether a “surprise alkane”—say made by explicit synthesis in a lab—is considered “interesting” probably depends first and foremost on whether it’s identified to have “interesting properties”. And that in turn tends to be a question of how its properties fit into the whole web of human knowledge and technology.
So can AI help in determining which alkanes we’re likely to consider interesting? Traditional computational chemistry—perhaps sped up by AI—can potentially determine the rates at which different alkanes are “randomly produced”. And in a quite different direction, analyzing the academic literature—say with an LLM—can potentially predict how much a certain alkane can be expected to be studied or talked about. Or (and this is particularly relevant for drug candidates) whether there are existing hints of “if only we could find a molecule that does ___” that one can pick up from things like academic literature.
As another example, let’s consider mathematical theorems. Much like with chemicals, one can in principle enumerate possible mathematical theorems by starting from axioms and then seeing what theorems can progressively be derived from them. Here’s what happens in just two steps starting from some typical axioms for logic:
There are a vast number of “uninteresting” (and often seemingly very pedantic) theorems here. But among all these there are two that are interesting enough that they’re typically given names (“the idempotence laws”) in textbooks of logic. Is there any way to determine whether a theorem will be given a name? One might have thought that would be a purely historical question. But at least in the case of logic there seems to be a systematic pattern. Let’s say one enumerates theorems of logic starting with the simplest, and going on in a lexicographic order. Most theorems in the list will be derivable from earlier ones. But a few will not. And these turn out to be basically exactly the ones that are typically given names (and highlighted here):
Or, in other words, at least in the rather constrained case of basic logic, the theorems considered interesting enough to be given names are the ones that “surprise us with new information”.
If we look more generally in “metamathematical space” we can get some empirical idea of where theorems that have been “considered interesting” lie:
Could an AI predict this? We could certainly create a neural net trained from the existing literature of mathematics, and its few million stated theorems. And we could then start feeding this neural net theorems found by systematic enumeration, and asking it to determine how plausible they are as things that might appear in mathematical literature. And in our systematic enumeration we could even ask the neural net to determine what “directions” are likely to be “interesting”—like in our second method for “AI-assisted traversal of multiway systems” above.
But when it comes to finding “genuinely new science” (or math) there’s a problem with this—because a neural net trained from existing literature is basically going to be looking for “more of the same”. Much like the typical operation of peer review, what it’ll “accept” is what’s “mainstream” and “not too surprising”. So what about the surprises that computational irreducibility inevitably implies will be there? By definition, they won’t be “easily reducible” to what’s been seen before.
Yes, they can provide new facts. And they may even have important applications. But there often won’t be—at least at first—a “human-accessible narrative” that “reaches” them. And what it’ll take to create that is for us humans to internalize some new concept that eventually becomes familiar. (And, yes, as we discussed above, if some particular new concept—or, say, new theorem—seems to be a “nexus” for reaching things, that becomes a target for a concept that’s worth us “adding”.)
But in the end, there’s a certain arbitrariness in which “new facts” or “new directions” we want to internalize. Yes, if we go in a particular direction it may lead us to certain ideas or technology or activities. But abstractly we don’t know which direction we might go is “right”; at least in the first instance, that seems like a quintessential matter of human choice. There’s a potential wrinkle, though. What if our AIs know enough about human psychology and society that they can predict “what we’d like”? At first it might seem that they could then successfully “pick directions”. But once again computational irreducibility blocks us—because ultimately we can’t “know what we’ll like” until we “get there”.
We can relate all this to generative AI, for example for images or text. At the outset, we might imagine enumerating images that consist of arbitrary arrays of pixels. But an absolutely overwhelming fraction of these won’t be at all “interesting” to us; they’ll just look to us like “random noise”:
By training a neural net on billions of human-selected images, we can get it to produce images that are somehow “generally like what we find interesting”. Sometimes the images produced will be recognizable to the point where we’ll be able to give a “narrative explanation” of “what they look like”:
But very often we’ll find ourselves with images “out in interconcept space”:
Are these “interesting”? It’s hard to say. Scanning the brain of a person looking at them, we might notice some particular signal—and perhaps an AI could learn to predict that. But inevitably that signal would change if some type of “interconcept image” become popular, and started, say, to be recognized as a kind of art that people are familiar with.
And in the end we’re back to the same point: things are ultimately “interesting” if our choices as a civilization make them so. There’s no abstract notion of “interestingness” that an AI or anything can “go out and discover” ahead of our choices.
And so it is with science. There’s no abstract way to know “what’s interesting” out of all the possibilities in the ruliad; that’s ultimately determined by the choices we make in “colonizing” the ruliad.
But what if—instead of going out into the “wilds of the ruliad”—we stay close to what’s already been done in science, and what’s already “deemed interesting”? Can AI help us extend what’s there? As a practical matter—at least when supplemented with our computational language as a tool—the answer is at some level surely yes. And for example LLMs should be able to produce things that follow the pattern of academic papers—with dashes of “originality” coming from whatever randomness is used in the LLM.
How far can such an approach get? The existing academic literature is certainly full of holes. Phenomenon A was investigated in system X, and B in Y, but not vice versa, etc. And we can expect that AIs—and LLMs in particular—can be useful in identifying these holes, and in effect “planning” what science is (by this criterion) interesting to do. And beyond this, we can expect that things like LLMs will be helpful in mapping out “usual and customary” paths by which the science should be done. (“When you’re analyzing data like this, one typically quotes such-and-such a metric”; “when you’re doing an experiment like this, you typically prepare a sample like this”; etc.) When it comes to actually “doing the science”, though, our actual computational language tools—together with things like computationally controlled experimental equipment—will presumably be what’s usually more central.
But let’s say we’ve defined some major objective for science (“figure out how to reverse aging”, or, a bit more modestly, “solve cryonics”). In giving such an objective, we’re specifying something we consider “interesting”. And then the problem of getting to that objective is—at least conceptually—like finding a proof of theorem or a synthesis pathway for a chemical. There are certain “moves we can make”, and we need to find out how to “string these together” to get to the objective we want. Inevitably, though, there’s an issue with (multi)computational irreducibility: there may be an irreducible number of steps we need to take to get to the result. And even though we may consider the final objective “interesting”, there’s no guarantee that we’ll find the intermediate steps even slightly interesting. Indeed, in many proofs—as well as in many engineering systems—one may need to build on an immense number of excruciating details to get to the final “interesting result”.
But let’s talk more about the question of what to study—or, in effect, what’s “interesting to study”. “Normal science” tends to be concerned with making incremental progress, remaining within existing paradigms, but gradually filling in and extending what’s there. Usually the most fertile areas are on the interfaces between existing well-developed areas. At the outset, it’s not at all obvious that different areas of science should ultimately fit together at all. But given the concept of the ruliad as the ultimate underlying structure, this begins to seem less surprising. Still, to actually see how different areas of science can be “knitted together” one will often have to identify—perhaps initially quite surprising—analogies between very different descriptive frameworks. “A decidable theory in metamathematics is like a black hole in physics”; “concepts in language are like particles in rulial space”; etc.
And this is an area where one can expect LLMs to be helpful. Having seen the “linguistic pattern” of one area, one can expect them to be able to see its correspondence in another area—potentially with important consequences.
But what about fresh new directions in science? Historically, these have often been the result of applying some new practical methodology (say for doing a new kind of experiment or measurement)—that happens to open up some “new place to look”, where people have never looked before. But usually one of the big challenges is to recognize that something one sees is actually “interesting”. And to do this often in effect involves the creation of some new conceptual framework or paradigm.
So can AI—as we’ve been discussing it here—be expected to do this? It doesn’t seem likely. AI is typically something trained on existing human material, intended to extrapolate directly from that. It’s not something built to “go out into the wilds of the ruliad”, far from anything already connected to humans.
But in a sense that is the domain of “arbitrary computation”, and of things like the simple programs we might enumerate or pick at random in ruliology. And, yes, by going out into the “wilds of the ruliad” it’s easy enough to find fresh, new things not currently assimilated into science. The challenge, though, is to connect them to anything we humans currently “understand” or “find interesting”. And that, as we’ve said before, is something that quintessentially involves human choice, and the foibles of human history. There are an infinite collection of paths that could be taken. (And indeed, in a “society of AIs”, there could be AIs that pursue a certain collection of them.) But in the end what matters to us humans and the enterprise we normally call “science” is our internal experience. And that’s something we ultimately have to form for ourselves.
Beyond the “Exact Sciences”
In areas like the physical sciences we’re used to the idea of being able to develop broad theories that can do things like make quantitative predictions. But there are many areas—for example in the biological, human and social sciences—that have tended to operate in much less formal ways, and where things like long chains of successful theoretical inferences are largely unheard of.
So might AI change that? There seem to be some interesting possibilities, particularly around the new kinds of “measurements” that AI enables. “How similar are those artworks?” “How close are the morphologies of those organisms?” “How different are those myths?” These are questions that in the past one mostly had to address by writing an essay. But now AI potentially gives us a path to make such things more definite—and in some sense quantitative.
Typically the key idea is to figure out how to take “unstructured raw data” and extract “meaningful features” from it that can be handled in formal, structured ways. And the main thing that makes this possible is that we have AIs that have been trained on large corpora that reflect “what’s typical in our world”—and which have in effect formed definite internal representations of the world, in terms of which things can for example be described (as we did above) by lists of numbers.
What do those numbers mean? At the outset we typically have no idea; they’re just the output of some neural net encoder. But what’s important is that they’re definite, and repeatable. Given the same input data, one will always get the same numbers. And, what’s more, it’s typical that when data “seems similar” to us, it’ll tend to be assigned nearby numbers.
In an area like physical science, we expect to build specific measuring devices that measure quantities we “know how to interpret”. But AI is much more of a black box: something is being measured, but at least at the outset we don’t necessarily have any interpretation of it. Sometimes we’ll be able to do training that associates some description we know, so that we’ll get at least a rough interpretation (as in a case like sentiment analysis). But often we won’t.
(And it has to be said that something similar can happen even in physical science. Let’s say we test whether one material scratches the surface of another. Presumably we can interpret that as some kind of hardness of the material, but really it’s just a measurement, that becomes significant if we can successfully associate it with other things.)
One thing that’s particularly notable about “AI measurements” is how they can potentially pick out “small signals” from large volumes of unstructured data. We’re used to having methods like statistics to do similar things on structured, numerical data. But it’s a different story to ask from billions of webpages whether, say, kids who like science typically prefer cats or dogs.
But given an “AI measurement” what can we expect to do with it? None of this is very clear yet, but it seems at least possible that we can start to find formal relationships. Perhaps it will be a quantitative relationship involving numbers; perhaps it will be better represented by a program that describes a computational process by which one measurement leads to others.
It’s been common for some time in areas like quantitative finance to find relationships between what amount to simple forms of “AI measurements”—and to be concerned mainly with whether they work, rather than why they work, or how one might narratively describe them.
In a sense it seems rather unsatisfactory to try to build science on “black-box” AI measurements that one can’t interpret. But at some level this is just an accelerated version of what we often do, say with everyday language. We’re exposed to some new observation or measurement. And eventually we invent words to describe it (“it looks like a fractal”, etc.). And then we can start “reasoning in terms of it”, etc.
But AI measurements are potentially a much richer source of formalizable material. But how should we do that formalization? Computational language seems to be key. And indeed we already have examples in the Wolfram Language—where functions like ImageIdentity or TextCases (or, for that matter, LLMFunction) can effectively make “AI measurements”, but then we can take their results, and work symbolically with them.
In physical science we often imagine that we’re working only with “objective measurements” (though my recent “observer theory” implies that actually our nature as observers is crucial even). But AI measurements seem to have a certain immediate “subjectivity”—and indeed their details (say, associated with the particulars of a neural net encoder) will be different for every different AI we use. But what’s important is that if the AI is trained on very large amounts of human experience, there’ll be a certain robustness to it. In a sense we can view many AI measurements as being like the output of a “societal observer”—that uses something like the whole mass of human experience, and in doing so gains a certain “centrality” and “inertia”.
What kind of science can we expect to build on the basis of what a “societal observer” measures? For the most part, we don’t yet know. There’s some reason to think that (as in the case of physics and metamathematics) such measurements might tap into pockets of computational reducibility. And if that’s the case, we can expect that we’ll be able to start doing things like making predictions—albeit perhaps only for the results of “AI measurements” which we’ll find hard to interpret. But by connecting such AI measurements to computational language, there seems to be the potential to start constructing “formalized science” in places where it’s never been possible before—and in doing so, to extend the domain of what we might call “exact sciences”.
(By the way, another promising application of modern AIs is in setting up “repeatable personas”: entities that effectively behave like humans with certain characteristics, but on which large-scale repeatable experiments of the kind typical in physical science can be done.)
So… Can AI Solve Science?
At the outset, one might be surprised that science is even possible. Why is it that there is regularity that we can identify in the world that allows us to form “scientific narratives”? Indeed, we now know from things like the concept of the ruliad that computational irreducibility is inevitably ubiquitous—and with it fundamental irregularity and unpredictability. But it turns out that the very presence of computational irreducibility necessarily implies that there must be pockets of computational reducibility, where at least certain things are regular and predictable. And it is within these pockets of reducibility that science fundamentally lives—and indeed that we try to operate and engage with the world.
So how does this relate to AI? Well, the whole story of things like trained neural nets that we’ve discussed here is a story of leveraging computational reducibility, and in particular computational reducibility that’s somehow aligned with what human minds also use. In the past the main way to capture—and capitalize on—computational reducibility was to develop formal ways to describe things, typically using mathematics and mathematical formulas. AI in effect provides a new way to make use of computational reducibility. Normally there’s no human-level narrative to how it works; it’s just that somehow within a trained neural net we manage to capture certain regularities that allow us, for example, to make certain predictions.
In a sense the predictions tend to be very “human style”, often looking “roughly right” to us, even though at the level of precise formal detail they’re not quite right. And fundamentally they rely on computational reducibility—and when computational irreducibility is present they more or less inevitably fail. In a sense, the AI is doing “shallow computation”, but when there’s computational irreducibility one needs irreducible, deep computation to work out what will happen.
And there are plenty of places—even in working with traditional mathematical structures—where what AI does won’t be sufficient for what we expect to get out of science. But there are also places where “AI-style science” can make progress even when traditional methods cannot. If one’s doing something like solving a single equation (say, ODE) precisely, AI probably won’t be the best tool. But if one’s got a big collection of equations (say for something like robotics) AI may successfully be able to give a useful “rough estimate” of what will happen, even when traditional methods would get utterly bogged down in details.
It’s a general feature of machine learning—and AI—techniques that they can be very useful if an approximate (“80%”) answer is good enough. But they tend to fail when one needs something more “precise” and “perfect”. And there are quite a few workflows in science (and probably more that can be identified) where this is exactly what one needs. “Pick out candidate cases for something”. “Identify a feature that might important”. “Suggest a possible question to explore”.
There are clear limitations, though, particularly whenever there’s computational irreducibility. In a sense the typical AI approach to science doesn’t involve explicitly “formalizing things”. But in many areas of science formalization is precisely what’s been most valuable, and what’s allowed towers of results to be obtained. And in recent times we have the powerful new idea of formalizing things computationally—and in particular in using computational language to do this.
And given such a computational formalization, we’re able to start doing irreducible computations that let us reach discoveries we have no way to anticipate. We can, for example, enumerate possible computational systems or processes, and see “fundamental surprises”. In typical AI there’s randomness that gives us a certain degree of “originality” in our exploration. But it’s of a fundamentally lower level than we can reach with actual irreducible computations.
So what should we expect for AI in science going forward? We’ve got in a sense a new—and rather human-like—way of leveraging computational reducibility. It’s a new tool for doing science, destined to have many practical uses. In terms of fundamental potential for discovery, though, it pales in comparison to what we can build from the computational paradigm, and from irreducible computations that we do. But probably what will give us the greatest opportunity to move science forward is to combine the strengths of AI and of the formal computational paradigm. Which, yes, is part of what we’ve been vigorously pursuing in recent years with the Wolfram Language and its connections to machine learning and now LLMs.
Notes
My goal here has been to outline my current thinking about the fundamental potential (and limitations) of AI in science—developing my ideas by using the Wolfram Language and its AI capabilities to do various simple experiments. I view what I’ve done here as just a beginning. Essentially every experiment could, for example, be done in much more detail, and with much more analysis. (And just click any image to get the Wolfram Language that made it, so you can repeat or extend it.)
“AI in science” is a hot topic these days in the world at large, and I am surely aware only of a small part of everything that’s been done. My own emphasis has been on trying to “do the obvious experiments” and trying to piece together for myself the “big picture” of what’s going on. I should emphasize that there’ve been a regular stream of outstanding and impressive “engineering innovations” in AI in recent times, and I won’t be at all surprised if experiments that haven’t worked well for me could be dramatically improved by future such innovations, conceivably even changing my “big-picture” conclusions from them.
I must also offer an apology. While I’ve been exposed—though often basically just “through the grapevine”—to lots of things being done on “AI in science”, especially over the past year, I haven’t made any serious attempt to systematically study the literature of the field, or trace its history and the provenance of ideas in it. So I must leave it to others to make connections between what I’ve done here and what other people may (or may not) have done elsewhere. It’d be fascinating to do a serious analysis of the history of work on AI in science, but it’s not something I’ve had a chance to do.
In my efforts here I have been greatly assisted by Wolfram Institute fellows Richard Assar (“Ruliad Fellow”) and Nik Murzin (“Fourmilab Fellow”). I’m also grateful to the many people who I’ve talked to—or heard from—about AI in science (and related topics) in recent times, including Giulio Alessandrini, Mohammed AlQuraishi, Brian Frezza, Roger Germundsson, George Morgan, Michael Trott and Christopher Wolfram.
]]>







 See also: “Computing the Eclipse: Astronomy in the Wolfram Language” » Updated and expanded from a post for the eclipse of August 21, 2017. Preparing for April 8, 2024 On April 8, 2024, there’s going to be a total eclipse of the Sun visible on a line across the US. But when exactly will the eclipse […]]]>
See also: “Computing the Eclipse: Astronomy in the Wolfram Language” » Updated and expanded from a post for the eclipse of August 21, 2017. Preparing for April 8, 2024 On April 8, 2024, there’s going to be a total eclipse of the Sun visible on a line across the US. But when exactly will the eclipse […]]]>











































 See also: “When Exactly Will the Eclipse Happen? A Multimillennium Tale of Computation” » Basic Eclipse Computation It’s taken millennia to get to the point where it’s possible to accurately compute eclipses. But now—as a tiny part of making “everything in the world” computable—computation about eclipses is just a built-in feature of the Wolfram Language. The […]]]>
See also: “When Exactly Will the Eclipse Happen? A Multimillennium Tale of Computation” » Basic Eclipse Computation It’s taken millennia to get to the point where it’s possible to accurately compute eclipses. But now—as a tiny part of making “everything in the world” computable—computation about eclipses is just a built-in feature of the Wolfram Language. The […]]]>












































































 Note: Click any diagram to get Wolfram Language code to reproduce it. Wolfram Language code for training the neural nets used here is also available (requires GPU). Won’t AI Eventually Be Able to Do Everything? Particularly given its recent surprise successes, there’s a somewhat widespread belief that eventually AI will be able to “do everything”, […]]]>
Note: Click any diagram to get Wolfram Language code to reproduce it. Wolfram Language code for training the neural nets used here is also available (requires GPU). Won’t AI Eventually Be Able to Do Everything? Particularly given its recent surprise successes, there’s a somewhat widespread belief that eventually AI will be able to “do everything”, […]]]>